题目内容
【题目】在矩形ABCD中,AB=2,BC=6,直线EF经过对角线BD的中点O,分别交边AD,BC于点E,F,点G,H分别是OB,OD的中点,当四边形EGFH为矩形时,则BF的长_________________.
【答案】![]() 或
或![]()
【解析】
根据矩形ABCD中,AB=2,BC=6,可求出对角线的长,再由点G、H分别是OB、OD的中点,可得GH=![]() BD,从而求出GH的长,若四边形EGFH为矩形时,EF=GH,可求EF的长,通过作辅助线,构造直角三角形,由勾股定理可求出MF的长,最后通过设未知数,列方程求出BF的长.
BD,从而求出GH的长,若四边形EGFH为矩形时,EF=GH,可求EF的长,通过作辅助线,构造直角三角形,由勾股定理可求出MF的长,最后通过设未知数,列方程求出BF的长.
解:如图:过点E作EM⊥BC,垂直为M,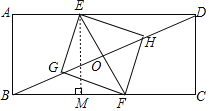
矩形ABCD中,AB=2,BC=6,
∴AB=EM=CD=2,AD=BC=6,∠A=90°,OB=OD,
在Rt△ABD中,BD=![]() =2
=2![]() ,
,
又∵点G、H分别是OB、OD的中点,
∴GH=![]() BD=
BD=![]() ,
,
当四边形EGFH为矩形时,GH=EF=![]() ,
,
在Rt△EMF中,FM=![]() =
=![]() ,
,
易证△BOF≌△DOE (AAS),
∴BF=DE,
∴AE=FC,
设BF=x,则FC=6-x,由题意得:x-(6-x)=![]() ,或(6-x)-x=
,或(6-x)-x=![]() ,,
,,
∴x=![]() 或x=
或x=![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目