题目内容
如图,E为正方形ABCD外一点,且△ADE为等边三角形,试求∠CEB的度数.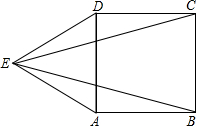
解:∵四边形ABCD为正方形,
∴AB=AD=CD,∠CDA=∠DAB=90°,
又∵△ADE为等边三角形,
∴AE=AD=DE,∠EDA=∠EAD=∠AED=60°,
∴AB=AE=CD=CE,∠EDC=∠EAB=150°,
∴△ABE和△DCE都为全等的等腰三角形,(4分)
∴∠AEB=∠DEC=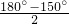 =15°,(6分)
=15°,(6分)
∴∠CEB=60°-15°-15°=30°.(8分)
分析:根据正方形的性质得到正方形ABCD四条边相等,四个角都为直角,又根据等边三角形的性质得到三角形ADE三条边相等,三个内角都相等,都为60°,等量代换得到AE=AB,DE=DC,即三角形EDC与三角形ABE都为等腰三角形且根据“SAS”得到两三角形全等,求出等腰三角形的顶角的度数,利用三角形的内角和定理求出底角的度数,然后由∠DAE的度数减去底角的度数的2倍可求出所求角的度数.
点评:此题考查了正方形的性质,等边三角形的性质,以及等腰三角形的性质与判定.熟练掌握正方形及等边三角形的性质是解本题的关键.
∴AB=AD=CD,∠CDA=∠DAB=90°,
又∵△ADE为等边三角形,
∴AE=AD=DE,∠EDA=∠EAD=∠AED=60°,
∴AB=AE=CD=CE,∠EDC=∠EAB=150°,
∴△ABE和△DCE都为全等的等腰三角形,(4分)
∴∠AEB=∠DEC=
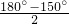 =15°,(6分)
=15°,(6分)∴∠CEB=60°-15°-15°=30°.(8分)
分析:根据正方形的性质得到正方形ABCD四条边相等,四个角都为直角,又根据等边三角形的性质得到三角形ADE三条边相等,三个内角都相等,都为60°,等量代换得到AE=AB,DE=DC,即三角形EDC与三角形ABE都为等腰三角形且根据“SAS”得到两三角形全等,求出等腰三角形的顶角的度数,利用三角形的内角和定理求出底角的度数,然后由∠DAE的度数减去底角的度数的2倍可求出所求角的度数.
点评:此题考查了正方形的性质,等边三角形的性质,以及等腰三角形的性质与判定.熟练掌握正方形及等边三角形的性质是解本题的关键.

练习册系列答案
相关题目
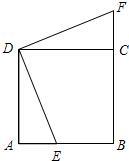 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以 向以
向以
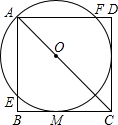 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.