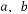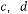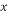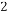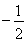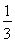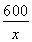题目内容
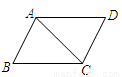
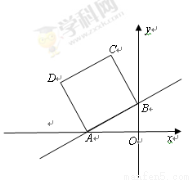
如图,在平面直角坐标系中,直线 +2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
(1)求点A、B的坐标,并求边AB的长;
(2)求点D和点C的坐标;
(3)你能否在x轴上找一点M,使△MDB的周长最小?如果能,请求出M点的坐标;如果不能,说明理由.
(1)(-4,0),(0,2),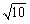 ;(2)(-6,4),(-2,6);(3)能,(-2,0).
;(2)(-6,4),(-2,6);(3)能,(-2,0).
【解析】
试题分析:(1)要求A,B点的坐标,实际上就是求一次函数与两坐标轴的交点问题,那么就令x=0及y=0可以求出A,B点的坐标,由此就可以求出AB的长度(2)要求点C,D的坐标首先需要证△DEA≌△AOB,证出OA=DE,AE=OB,即可求出D的坐标,同理可以求出点C的坐标;(3)先作出D关于X轴的对称点F,连接BF,BF于X轴交点M就是符合条件的点,求出F的坐标,进而求出直线BF,再求出与X轴交点即可.
试题解析:【解析】
(1)当y=0时,x=-4, 则A的坐标(-4,0),
当x=0时,y=2 ,则B的坐标(0,2),
∴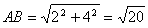 ;
;
(2)过D做线段DE垂直x轴,交x轴与E
则△DEA≌△AOB ,
∴DE=AO=4,EA=OB=2
∴D的坐标为(-6,4),
同理可得C的坐标为(-2,6); (3)作B关于x轴的对称点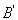 ,连接M
,连接M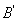 ,与x轴的交点即为点M,则
,与x轴的交点即为点M,则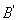 (0,-2),设直线M
(0,-2),设直线M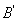 的解析式为
的解析式为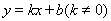 ,则有
,则有
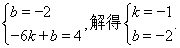
 直线M
直线M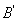 的解析式为
的解析式为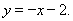
当y=0,x=-2,则M的坐标为(-2,0).
考点:1. 一次函数综合题2.全等三角形的性质及判定.

甲、乙两车间生产同一种零件,乙车间比甲车间每小时多生产30个,甲车间生产600个零件与乙车间生产900个零件所用时间相等.设甲车间平均每小时生产x个零件,请按要求解决下列问题:
(1)根据题意,填写下表:
车间 | 零件总个数 | 平均每小时生产 零件个数 | 所用时间 |
甲车间 | 600 | x |
|
乙车间 | 900 |
|
|
(2)甲车间平均每小时生产多少个零件?
(3)若甲车间生产零件的总个数是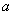 (0<
(0<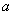 <900 )个,题目中的其它条件不变,则甲车间每小时生产的零件是 个(结果用
<900 )个,题目中的其它条件不变,则甲车间每小时生产的零件是 个(结果用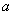 表示).
表示).