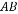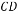Question

已知一次函数y=kx+b的图象经过点（-2，-4），且与正比例函数y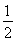＝x的图象相交于点（4，a），求：
（1）a的值；
（2）k、b的值；
（3）这两个函数的图象与y轴相交得到的三角形的面积．

 

Answer 1

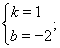（1）2；（2）（3）4.

【解析】

试题分析：（1）要求的a值，就需要把点（4，a）代入正比例函数y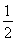＝x中即可以求得a的值；（2）要求出字母k,b的值，就需要把点（-2，-4），点（4，a），代入一次函数y=kx+b中即可得k，b的值；（3）根据根据求出的两个函数图象，画出相关喊出图像即可得到图形，与它们与y轴相交得到的三角形的面积等于（2）得到的直线与y轴的交点的绝对值与两直线交点的横坐标的积的一半．

试题解析：（1）（1）将点（4，a）代入正比例函数y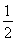＝x，
解得a=2；

(2)将点（4,2）、（-2，-4）分别代入y=kx+b得：

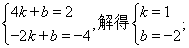
（3）画出图形如下：

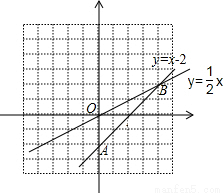
直线y=x-2交y轴于点（0，-2）， ∴围成的三角形的面积为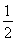×2×4=4．

考点：两条直线相交或平行问题．