题目内容
 已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?
已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?
解:设P,Q同时出发t秒后四边形PDCQ或四边形APQB是平行四边形,根据已知得到AP=t,PD=24-t,CQ=2t,BQ=30-2t.
(1)若四边形PDCQ是平行四边形,则PD=CQ,∴24-t=2t,∴t=8,∴8秒后四边形PDCQ是平行四边形;
(2)若四边形APQB是平行四边形,则AP=BQ,∴t=30-2t,∴t=10,∴10秒后四边形APQB是平行四边形.
∴出发后10秒或8秒其中一个是平行四边形.
分析:若四边形PDCQ或四边形APQB是平行四边形,那么QD=CQ或AP=BQ或PD=BQ,根据这个结论列出方程就可以求出时间.
点评:此题主要考查了平行四边形的性质与判定,不过用运动的观点结合梯形的知识出题学生不是很适应.
(1)若四边形PDCQ是平行四边形,则PD=CQ,∴24-t=2t,∴t=8,∴8秒后四边形PDCQ是平行四边形;
(2)若四边形APQB是平行四边形,则AP=BQ,∴t=30-2t,∴t=10,∴10秒后四边形APQB是平行四边形.
∴出发后10秒或8秒其中一个是平行四边形.
分析:若四边形PDCQ或四边形APQB是平行四边形,那么QD=CQ或AP=BQ或PD=BQ,根据这个结论列出方程就可以求出时间.
点评:此题主要考查了平行四边形的性质与判定,不过用运动的观点结合梯形的知识出题学生不是很适应.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.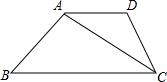 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,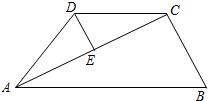 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE= (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.