题目内容
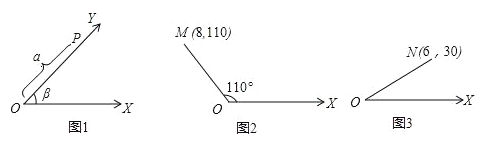
【题目】如图1，将射线OX按逆时针方向旋转β角，得到射线OY，如果点P为射线OY上的一点，且OP=a，那么我们规定用（a，β）表示点P在平面内的位置，并记为P（a，β），例如，图2中，如果OM=8，∠XOM=110°，那么点M在平面内的位置，记为M（8，110），根据图形，解答下面的问题：
（1）如图3，如果点N在平面内的位置记为N（6，30），那么ON= ；∠XON= ．
（2）如果点A、B在平面内的位置分别记为A（5，30），B（12，120），试求A、B两点之间的距离并画出图．
【答案】（1）6，30°；（2）13．
【解析】试题分析：（1）由题意得第一个坐标表示此点距离原点的距离，第二个坐标表示此点与原点的连线与x轴所夹的角的度数；
（2）根据相应的度数判断出△AOB的形状，再利用勾股定理得出AB的长．
试题解析：（1）根据点N在平面内的位置极为N（6，30）可知，ON=6，∠XON=30°．
（2）如图所示：
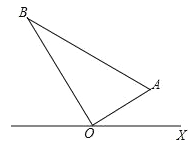
∵A（5，30），B（12，120），
∴∠BOX=120°，∠AOX=30°，
∴∠AOB=90°，
∵OA=5，OB=12，
∴在Rt△AOB中，AB=
练习册系列答案
相关题目
