题目内容
【题目】如图，Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．
（1）若△BPQ与△ABC相似，求t的值；
（2）连接AQ、CP，若AQ⊥CP，求t的值．
【答案】
（1）解：∵Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，
∴由勾股定理可得：BA= 
；
由题意现分两种情况讨论：
①当△BPQ∽△BAC时， 
，
∵BP=5t，QC=4t，AB=10，BC=8，
∴ 
，解得： 
；
②当△BPQ∽△BCA时， 
，
∴ 
，解得， 
；
综上所述，当 或 时，△BPQ与△ABC相似
（2）解：过P作PM⊥BC于点M，AQ，CP交于点N，如图1所示：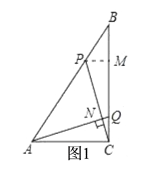
∴∠PMB=∠ACB=90°，
∴PM∥AC，
∴△BPM∽△BAC，
∴ 
，即 
，
∴PM= 
，BM= 
，
∴CM= 
.
∵AQ⊥CP，∠ACB=90°，
∵∠NAC+∠NCA=90°，∠PCM+∠NCA=90°，
∴∠NAC=∠PCM，
∵∠ACQ=∠PMC，
∴△ACQ∽△CMP，
∴ 
，即 
，解得 
【解析】（1）根据勾股定理即可得到结论；分两种情况：①当△BPQ∽△BAC时，BP：BA=BQ：BC；当△BPQ∽△BCA时，BP：BC=BQ：BA，再根据BP=5t，QC=4t，AB=10cm，BC=8cm，代入计算即可；
（2）分三种情况：①当PB=PQ时，如图1，过P作PH⊥BQ，根据平行线分线段成比例定理得到，②当PB=BQ时，即5t=8-4t，，③当BQ=PQ时，如图2，过Q作QG⊥AB于G，BQ=8-4t，通过△BGQ∽△ACB，得到比例式
【考点精析】认真审题，首先需要了解相似三角形的应用(测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解)．
