题目内容
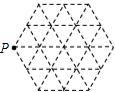如图，在由24个边长都为1的小正三角形的网格中，点P是正六边形的一个顶点，Q在网格中的格点（即小正三角形的顶点）上，若以点P，Q为端点的线段的长为无理数，请你写出所有可能的线段PQ的长分析：首先根据勾股定理求得P到各个格点之间的距离，然后即可确定．
解答：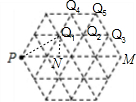
解：每个小正三角形的高是：
．
则过Q1作PM的垂线Q1N，
则PQ1=
，可得：NQ1=
；
同理可得：PQ2=
；PQ3=
；PQ4=
；PQ5=2
，
则PQ的长是：
或
或
或
或2
．
故答案是：
或
或
或
或2
解：每个小正三角形的高是：
| ||
| 2 |
则过Q1作PM的垂线Q1N，
则PQ1=
| 3 |
| ||
| 2 |
同理可得：PQ2=
| ||
| 2 |
| 13 |
| 7 |
| 3 |
则PQ的长是：
| 3 |
| ||
| 2 |
| 7 |
| 13 |
| 3 |
故答案是：
| 3 |
| ||
| 2 |
| 7 |
| 13 |
| 3 |
点评：本题主要考查了勾股定理的应用，求得P到各个格点的距离是解题关键．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
如图，在由24个边长都为1的小正三角形组成的正六边形网格中，以格点P为直角顶点作格点直角三角形（即顶点均在格点上的三角形），请你写出所有可能的直角三角形斜边的长
