题目内容
(2007•金华)如图,在由24个边长都为1的小正三角形组成的正六边形网格中,以格点P为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长 .
【答案】分析:在正六面体中,首先找出以点P为直角的直角三角形,然后应用勾股定理求其斜边长.
解答: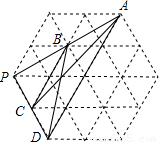 解:通过作图,知以点P为直角的三角形由四种情况,
解:通过作图,知以点P为直角的三角形由四种情况,
如上图,△PCB、△PCA、△PDB、△PDA,均是以点P为直角的直角三角形,
故:在Rt△PCB中,BC=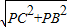 =
=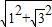 =2;
=2;
在Rt△PCA中,AC=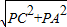 =
=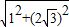 =
=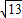 ;
;
在Rt△PDB中,BD=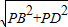 =
=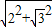 =
=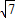 ;
;
在Rt△PAD中,AD=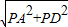 =
=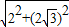 =4.
=4.
故所有可能的直角三角形斜边的长为4,2,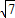 ,
,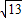 .
.
点评:本题主要考查勾股定理的应用,难易程度适中.
解答:
 解:通过作图,知以点P为直角的三角形由四种情况,
解:通过作图,知以点P为直角的三角形由四种情况,如上图,△PCB、△PCA、△PDB、△PDA,均是以点P为直角的直角三角形,
故:在Rt△PCB中,BC=
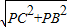 =
=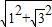 =2;
=2;在Rt△PCA中,AC=
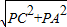 =
=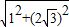 =
=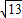 ;
;在Rt△PDB中,BD=
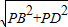 =
=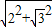 =
=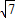 ;
;在Rt△PAD中,AD=
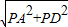 =
=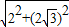 =4.
=4.故所有可能的直角三角形斜边的长为4,2,
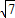 ,
,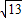 .
.点评:本题主要考查勾股定理的应用,难易程度适中.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN. 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值. ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.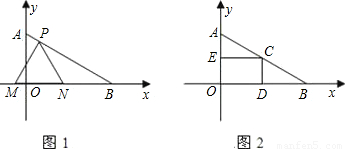 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值. ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN. 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值. ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN. 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值. ),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒
),点B在x正半轴上,且∠ABO=30度.动点P在线段AB上从点A向点B以每秒 个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN.
个单位的速度运动,设运动时间为t秒.在x轴上取两点M,N作等边△PMN. 出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.
出当0≤t≤2秒时S与t的函数关系式,并求出S的最大值.