��Ŀ����
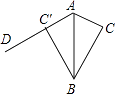
����Ŀ����֪O��ֱ��AB��һ������һֱ�����dz���ͼQZ��13(a)������һֱ�DZ�ON��ֱ��AB������һֱ�DZ�OM��AB���γɵġ�AOM��90�㣬����OC�ڡ�AOM�ڲ�.
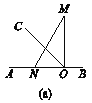

��̽������ͼ(b)�������dz����ŵ�O˳ʱ����ת������AON����CONʱ�����ж�OM�Ƿ�ƽ�֡�BOC����˵������.
����չ������AOC��80��ʱ�����dz�OMN��O��˳ʱ����תһ����ÿ����ת5�㣬������������MOC����MOB?
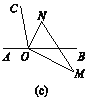
�����죩����������������ͼ(c)����ת���dz�ʹON�ڡ�BOC�ڲ�����һ��OM��ֱ��AB����һ���������������ۣ��١�NOC����BOM��ֵ���䣻�ڡ�NOC����BOM��ֵ���䣮ѡ������һ����ȷ�Ľ���˵�����ɣ�
���𰸡���̽����DMƽ�֡�BOC�����ɼ�����������չ��8���44���MOC����MOB�������졿�ٽ�����ȷ�����ɼ�����.
��������
��1������ͼ�κ�����ó���AON+��BOM=90�㣬��CON+��COM=90�㣬�ٸ��ݡ�AON=��CON�����ɵó�OMƽ�֡�BOC��
��2�����ݡ�AOC=80�b���ٷ�����������ۣ������ǰ�OMN��O��˳ʱ����ת40��ʱ����MOC=��MOB�����ǰ�OMN��O��˳ʱ����ת220��ʱ����MOC=��MOB���Ӷ��ó��𰸣�
��3���ֱ������NOC=100��-��BON����BOM=90��-��BON���ó���NOC-��BOM=10�㼴�ɣ�
̽��:DMƽ�֡�BOC.
���ɣ���Ϊ��AON����BOM��90������CON����COM��90������AON����CON, ��
���ԡ�COM����BOM��
����OMƽ�֡�BOC.
��չ:�����������
��Ϊ��AOC��80���� �ٵ����dz�OMN��O��˳ʱ����ת40��ʱ����MOC����MOB��
����40���5��8(��); �ڵ����dz�OMN��O��˳ʱ����ת220��ʱ����MOC����MOB��
����220���5��44(��).
����������8���44���MOC����MOB.
����:�ٽ�����ȷ�����ɣ�
����NOC��180������AOC����BON��100������BON����BOM��90������BON,
���ԡ�NOC����BOM��(100������BON)��(90������BON)��10����
���Ԣ١�NOC����BOM��ֵ������ȷ��

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�