题目内容
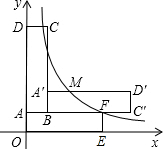 两个完全相同的矩形ABCD、AOEF按如图所示的方式摆放,使点A、D均在y轴的正半轴上,点B在第一象限,点E在x轴的正半轴上,点F在函数y=
两个完全相同的矩形ABCD、AOEF按如图所示的方式摆放,使点A、D均在y轴的正半轴上,点B在第一象限,点E在x轴的正半轴上,点F在函数y=| k |
| x |
(1)求k的值.
(2)将矩形ABCD绕点B顺时针旋转90°得到矩形A'BC'D',边A'D交函数y=
| k |
| x |
分析:(1)先求出点F的坐标,后代入双曲线的解析式即可求出k的值;
(2)先求出点M和点D'的坐标,继而求得MD'的长.
(2)先求出点M和点D'的坐标,继而求得MD'的长.
解答:解:(1)由已知得:点F(4,1),(2分)
又∵点F在y=
(x>0)上,
∴1=
,
∴k=4.(4分)
(2)由已知得:D'(5,2).(6分)
设点M(m,2),∵点M在双曲线y=
(x>0)上,
∴2=
,m=2,M(2,2).(8分)
∴MD'=5-2=3.(10分)
又∵点F在y=
| k |
| x |
∴1=
| k |
| 4 |
∴k=4.(4分)
(2)由已知得:D'(5,2).(6分)
设点M(m,2),∵点M在双曲线y=
| 4 |
| x |
∴2=
| 4 |
| m |
∴MD'=5-2=3.(10分)
点评:本题考查了反比例函数的综合运用,难度不大,注意根据题给条件求出关键点的坐标是关键.

练习册系列答案
相关题目
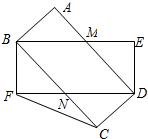 20、两个完全相同的矩形纸片ABCD、BFDE如图放置,AB=BF.请判断四边形BNDM的形状,并给出证明.
20、两个完全相同的矩形纸片ABCD、BFDE如图放置,AB=BF.请判断四边形BNDM的形状,并给出证明. 两个完全相同的矩形纸片ABCD、BFDE如图放置,AB=BF.
两个完全相同的矩形纸片ABCD、BFDE如图放置,AB=BF. 两个完全相同的矩形ABCD、AOEF按如图所示的方式摆放,使点A、D均在y轴的正半轴上,点B在第一象限,点E在x轴的正半轴上,点F在函数y=
两个完全相同的矩形ABCD、AOEF按如图所示的方式摆放,使点A、D均在y轴的正半轴上,点B在第一象限,点E在x轴的正半轴上,点F在函数y=