题目内容
【题目】如图，一次函数y=kx+b（k＜0）与反比例函数y= 
的图象相交于A、B两点，一次函数的图象与y轴相交于点C，已知点A（4，1） 
（1）求反比例函数的解析式；
（2）连接OB（O是坐标原点），若△BOC的面积为3，求该一次函数的解析式．
【答案】
（1）
解：∵点A（4，1）在反比例函数y= 
的图象上，
∴m=4×1=4，
∴反比例函数的解析式为y= 
．
（2）
解：∵点B在反比例函数y= 的图象上，
∴设点B的坐标为（n， 
）．
将y=kx+b代入y= 中，得：
kx+b= ，整理得：kx2+bx﹣4=0，
∴4n=﹣ 
，即nk=﹣1①．
令y=kx+b中x=0，则y=b，
即点C的坐标为（0，b），
∴S△BOC= 
bn=3，
∴bn=6②．
∵点A（4，1）在一次函数y=kx+b的图象上，
∴1=4k+b③．
联立①②③成方程组，即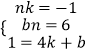 
，
解得：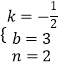 
，
∴该一次函数的解析式为y=﹣ x+3．
【解析】（1）由点A的坐标结合反比例函数系数k的几何意义，即可求出m的值；
（2）设点B的坐标为（n， ），将一次函数解析式代入反比例函数解析式中，利用根与系数的关系可找出n、k的关系，由三角形的面积公式可表示出来b、n的关系，再由点A在一次函数图象上，可找出k、b的关系，联立3个等式为方程组，解方程组即可得出结论．本题考查了反比例函数与一次函数交点的问题、反比例函数系数k的几何意义、三角形的面积公式以及根与系数的关系，解题的关键是：（1）利用反比例函数系数k的几何意义求出m的值；（2）根据各关系量找出关于k、b、n的三元一次方程组．本题属于中档题，难度不大，但考到的知识点较多，解决该题型题目时，综合根与系数的关系、三角形的面积公式以及一次函数上点的坐标特征得出方程组是关键．
【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，从该地区随机抽取部分七年级学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名同学只能选择其中一类节目），并调查得到的数据用下面的表和扇形图来表示（表、图都没制作完成）
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 36 | 90 | a | b | 27 |
根据表、图提供的信息，解决以下问题：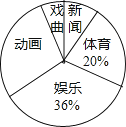
（1）计算出表中a、b的值；
（2）求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数；
（3）若该地区七年级学生共有47500人，试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人？
