题目内容
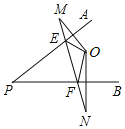
【题目】如图,已知点O是∠APB内的一点,M,N分别是点O关于PA、PB的对称点,连接MN,与PA、PB分别相交于点E、F,已知MN=6cm.
(1)求△OEF的周长;
(2)连接PM、PN,若∠APB=ɑ,求∠MPN(用含ɑ的代数式表示);
(3)当∠ɑ=30°,判定△PMN的形状,并说明理由.
【答案】(1)△OEF的周长是6cm;(2)∠MPN=2ɑ;(3)△PMN是等边三角形,理由见解析.
【解析】试题分析:(1)根据轴对称的性质把△OEF的周长转化为MN的长度,根据题意即能得出△OEF的周长;
(2)根据轴对称的性质可得∠MPA=∠OPA,∠NPB=∠OPB,从而可得;
(3)由(2)可得∠MPN=60°,由轴对称的性质可得PM=PN,从而可得△PMN是等边三角形.
试题解析:(1)∵M,N分别是点O关于PA、PB的对称点,
∴EM=EO,FN=FO,
∴△OEF的周长=OE+OF+EF=ME+EF+FN=MN=6cm;
(2)连接OP,
∵M,N分别是点O关于PA、PB的对称点,
∴∠MPA=∠OPA,∠NPB=∠OPB,
∴∠MPN=2∠APB=2ɑ;
(3)△PMN是等边三角形,理由如下:
∵∠ɑ=30°,
∴∠MPN=60°,
∵M,N分别是点O关于PA、PB的对称点,
∴PM=PO,PN=PO,
∴PM=PN,
∴△PMN是等边三角形.

练习册系列答案
相关题目


