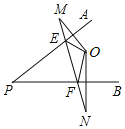
题目内容
【题目】如图,在△ABC中,AB=AC,取点D与点E,使得AD=AE,∠BAE=∠CAD,连结BD与CE交于点O.求证:

(1)△ABD≌△ACE;
(2)OB=OC.
【答案】见解析
【解析】
试题分析:(1)由已知条件得到∠BAD=∠CAE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到∠ABD=∠ACE,由等腰三角形的性质得到∠ABC=∠ACB由角的和差即可得到∠OBC=∠OCB,然后根据等腰三角形的判定即可得到结论.
证明:(1)∵∠BAE=∠CAD,
∴∠BAD=∠CAE,
在△ABD与△ACE中,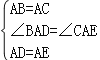 ,
,
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB
∴∠ABC﹣∠ABD=∠ACB﹣∠ACE,
即∠OBC=∠OCB,
∴OB=OC.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】某班学生经常采用“小组合作学习”的方式进行学习,王老师每周对各小组合作学习的情况进行综合评分.下表是各小组其中一周的得分情况:
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 |
得分 | 90 | 95 | 90 | 88 | 90 | 92 | 85 | 90 |
这组数据的众数是_____.