Question

【题目】如图，一次函数y1=kx+b和反比例函数y2= 的图象交于A、B两点．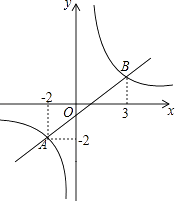

（1）求一次函数y1=kx+b和反比例函数y2= 的解析式；
（2）观察图象写出y1＜y2时，x的取值范围为；
（3）求△OAB的面积．

Answer 1

【答案】
（1）解：由图可知：A（﹣2，﹣2），

∵反比例函数y2= 的图象过点A（﹣2，﹣2），

∴m=4，

∴反比例函数的解析式是：y2= ，

把x=3代入得，y= ，

∴B（3， ），

∵y=kx+b过A、B两点，

∴

解得：k= ，b=﹣ ，

∴一次函数的解析式是：y1= x﹣

（2）x＜﹣2或0＜x＜3
（3）解：由一次函数y1= x﹣ 可知直线与y轴的交点为（0，﹣ ），

∴△OAB的面积= × ×2+ × ×3=

【解析】（1）由图可知：A（﹣2，﹣2），

∵反比例函数y2= 的图象过点A（﹣2，﹣2），

∴m=4，

∴反比例函数的解析式是：y2= ，

把x=3代入得，y= ，

∴B（3， ），

∵y=kx+b过A、B两点，

∴

解得：k= ，b=﹣ ，

∴一次函数的解析式是：y1= x﹣

（2）根据图象可得：当x＜﹣2或0＜x＜3时，y1＜y2．
由一次函数 可知直线与y轴的交点为（0，﹣ 2 3 ），

∴△OAB的面积= × ×2+ × ×3=

所以答案是：（1）；;（2）x＜﹣2或0＜x＜3；（3）.