ЬтФПФкШн
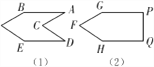
ЁОЬтФПЁПШчЭМЃЌЁїABCКЭЁїDEFЪЧСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌЁЯBAC=ЁЯEDF=90ЁуЃЌЁїDEFЕФЖЅЕуEгыЁїABCЕФаББпBCЕФжаЕужиКЯЃЎНЋЁїDEFШЦЕуEа§зЊЃЌа§зЊЙ§ГЬжаЃЌЯпЖЮDEгыЯпЖЮABЯрНЛгкЕуPЃЌЯпЖЮEFгыЩфЯпCAЯрНЛгкЕуQЃЎ
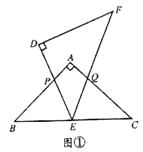
ЃЈ1ЃЉШчЭМЂйЃЌЕБЕуQдкЯпЖЮACЩЯЃЌЧвAP=AQЪБЃЌЧѓжЄЃКЁїBPEЁеЁїCQEЃЛ
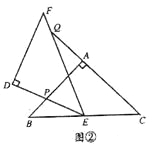
ЃЈ2ЃЉШчЭМЂкЃЌЕБЕуQдкЯпЖЮCAЕФбгГЄЯпЩЯЪБЃЌЧѓжЄЃКЁїBPEЁзЁїCEQЃЛВЂЧѓЕБBP= ![]() ЃЌCQ=
ЃЌCQ= ![]() ЪБЃЌPЁЂQСНЕуМфЕФОрРы (гУКЌ
ЪБЃЌPЁЂQСНЕуМфЕФОрРы (гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЎ
ЕФДњЪ§ЪНБэЪО)ЃЎ
ЁОД№АИЁПЃЈ1ЃЉгЩЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌвзЕУЁЯB=ЁЯC=45ЁуЃЌAB=ACЃЌгжгЩAP=AQЃЌEЪЧBCЕФжаЕуЃЌРћгУSASЃЌПЩжЄЕУЁїBPEЁеЁїCQEЃЛ
ЃЈ2ЃЉгЩЁїABCКЭЁїDEFЪЧСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌвзЕУЁЯB=ЁЯC=ЁЯDEF=45ЁуЃЌШЛКѓРћгУШ§НЧаЮЕФЭтНЧЕФаджЪЃЌМДПЩЕУЁЯBEP=ЁЯEQCЃЌдђПЩжЄЕУЁїBPEЁзЁїCEQЃЛPQ=![]() a
a
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌвзЕУЁЯB=ЁЯC=45ЁуЃЌAB=ACЃЌгжгЩAP=AQЃЌEЪЧBCЕФжаЕуЃЌРћгУSASЃЌПЩжЄЕУЃКЁїBPEЁеЁїCQEЃЛ
ЃЈ2ЃЉгЩЁїABCКЭЁїDEFЪЧСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌвзЕУЁЯB=ЁЯC=ЁЯDEF=45ЁуЃЌШЛКѓРћгУШ§НЧаЮЕФЭтНЧЕФаджЪЃЌМДПЩЕУЁЯBEP=ЁЯEQCЃЌдђПЩжЄЕУЃКЁїBPEЁзЁїCEQЃЛИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУBEЕФГЄЃЌМДПЩЕУBCЕФГЄЃЌМЬЖјЧѓЕУAQгыAPЕФГЄЃЌРћгУЙДЙЩЖЈРэМДПЩЧѓЕУPЁЂQСНЕуМфЕФОрРыЃЎ
ЁпЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯB=ЁЯC=45ЁуЃЌAB=ACЃЌ
ЁпAP=AQЃЌ
ЁрBP=CQЃЌ
ЁпEЪЧBCЕФжаЕуЃЌ
ЁрBE=CEЃЌ
ЁрЁїBPEЁеЁїCQEЃЈSASЃЉЃЛ
ЃЈ2ЃЉСЌНгPQ
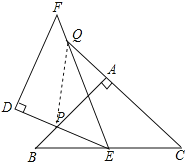
ЁпЁїABCКЭЁїDEFЪЧСНИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯB=ЁЯC=ЁЯDEF=45ЁуЃЌ
ЁпЁЯBEQ=ЁЯEQC+ЁЯCЃЌМДЁЯBEP+ЁЯDEF=ЁЯEQC+ЁЯCЃЌ
ЁрЁЯBEP+45Ёу=ЁЯEQC+45ЁуЃЌ
ЁрЁЯBEP=ЁЯEQCЃЌ
ЁрЁїBPEЁзЁїCEQЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпBP=aЃЌCQ=![]() aЃЌBE=CEЃЌ
aЃЌBE=CEЃЌ
Ёр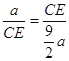 ЃЌ
ЃЌ
ЁрBE=CE=![]() ЃЌ
ЃЌ
ЁрBC=3![]() ЃЌ
ЃЌ
ЁрAB=AC=BCsin45Ёу=3aЃЌ
ЁрAQ=CQ-AC=![]() ЃЌPA=AB-BP=2aЃЌ
ЃЌPA=AB-BP=2aЃЌ
![]()