题目内容
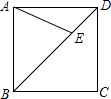 如图,E为正方形ABCD对角线BD上的一点,且BE=BC,则∠DAE=________.
如图,E为正方形ABCD对角线BD上的一点,且BE=BC,则∠DAE=________.
22.5°
分析:由正方形的性质得到AB=BC,∠DAB=∠ABC=90°,∠ABD=∠DBC=45°,推出AB=BE,根据三角形的内角和定理求出∠BAE=∠BEA=67.5°,根据∠DAE=∠DAB-∠BAE即可求出答案.
解答:∵正方形ABCD,
∴AB=BC,∠DAB=∠ABC=90°,
∴∠ABD=∠DBC= ∠ABC=45°,
∠ABC=45°,
∵BE=BC,
∴AB=BE,
∴∠BAE=∠BEA= (180°-∠ABD)=67.5°,
(180°-∠ABD)=67.5°,
∴∠DAE=∠DAB-∠BAE=90°-67.5°=22.5°,
故答案为:22.5°.
点评:本题主要考查对正方形的性质,三角形的内角和定理,等腰三角形的性质等知识点的理解和掌握,能根据这些性质求出∠BAE的度数是解此题的关键,题型较好,难度适中.
分析:由正方形的性质得到AB=BC,∠DAB=∠ABC=90°,∠ABD=∠DBC=45°,推出AB=BE,根据三角形的内角和定理求出∠BAE=∠BEA=67.5°,根据∠DAE=∠DAB-∠BAE即可求出答案.
解答:∵正方形ABCD,
∴AB=BC,∠DAB=∠ABC=90°,
∴∠ABD=∠DBC=
 ∠ABC=45°,
∠ABC=45°,∵BE=BC,
∴AB=BE,
∴∠BAE=∠BEA=
 (180°-∠ABD)=67.5°,
(180°-∠ABD)=67.5°,∴∠DAE=∠DAB-∠BAE=90°-67.5°=22.5°,
故答案为:22.5°.
点评:本题主要考查对正方形的性质,三角形的内角和定理,等腰三角形的性质等知识点的理解和掌握,能根据这些性质求出∠BAE的度数是解此题的关键,题型较好,难度适中.

练习册系列答案
相关题目
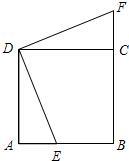 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.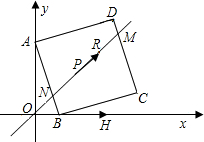 OM方向以
OM方向以 向以
向以
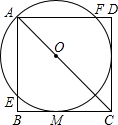 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.