��Ŀ����
��2013•÷�ݣ�����ͼ�٣�����ʾ������ֱ�������Σ����ֱ߳����ǵĶ�����ͼ���ѱ�����������������̽�����⣺

̽��һ��������������������ͼ��ƴ�ӣ�BC��ED�غϣ�����BC������һ����P��
��1������P�˶�����CFB�Ľ�ƽ������ʱ������AP�����߶�AP�ij���
��2������P���˶��Ĺ����г���PA=FCʱ�����PAB�Ķ�����
̽��������ͼ�ܣ�����DEF�Ķ���D���ڡ�ABC��BC���ϵ��е㴦�����Ե�DΪ��ת������ת��DEF��ʹ��DEF����ֱ�DZ����ABC����ֱ�DZ߷ֱ���M��N���㣬����MN������ת��DEF�Ĺ����У���AMN���ܳ��Ƿ��������Сֵ�������ڣ����������Сֵ���������ڣ���˵�����ɣ�


̽��һ��������������������ͼ��ƴ�ӣ�BC��ED�غϣ�����BC������һ����P��
��1������P�˶�����CFB�Ľ�ƽ������ʱ������AP�����߶�AP�ij���
��2������P���˶��Ĺ����г���PA=FCʱ�����PAB�Ķ�����
̽��������ͼ�ܣ�����DEF�Ķ���D���ڡ�ABC��BC���ϵ��е㴦�����Ե�DΪ��ת������ת��DEF��ʹ��DEF����ֱ�DZ����ABC����ֱ�DZ߷ֱ���M��N���㣬����MN������ת��DEF�Ĺ����У���AMN���ܳ��Ƿ��������Сֵ�������ڣ����������Сֵ���������ڣ���˵�����ɣ�

��������1�����ͼ1��ʾ������A��AG��BC�ڵ�G������Rt��APG�����ù��ɶ������AP�ij��ȣ�
��2�����ͼ2��ʾ�����������ĵ�P����������ֱ�������Σ���������ǵ����Ǻ���ֵ����ǵĶ�����
��3�����ͼ3��ʾ��֤����AMD�ա�CND����AM=CN�����AMN��ֱ�DZ߳���֮��Ϊ��ֵ����AM=x�����б��MN�ı���ʽ�����ö��κ������������MN����Сֵ���Ӷ��õ���AMN�ܳ�����Сֵ��
��2�����ͼ2��ʾ�����������ĵ�P����������ֱ�������Σ���������ǵ����Ǻ���ֵ����ǵĶ�����
��3�����ͼ3��ʾ��֤����AMD�ա�CND����AM=CN�����AMN��ֱ�DZ߳���֮��Ϊ��ֵ����AM=x�����б��MN�ı���ʽ�����ö��κ������������MN����Сֵ���Ӷ��õ���AMN�ܳ�����Сֵ��
����⣺̽��һ����1�������⻭��ͼ�Σ����ͼ1��ʾ��

�����⣬�á�CFB=60�㣬FPΪ��ƽ���ߣ����CFP=30�㣬
��CF=BC•tan30��=3��
=
��
��CP=CF•tan��CFP=
��
=1��
����A��AG��BC�ڵ�G����AG=
BC=
��
��PG=CG-CP=
-1=
��
��Rt��APG�У��ɹ��ɶ����ã�
AP=
=
=
��
��2���ɣ�1����֪��FC=
��
���ͼ2��ʾ���Ե�AΪԲ�ģ���FC=
��Ϊ�뾶��������BC���ڵ�P1��P2����AP1=AP2=
��
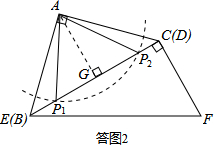
����A��AG��BC�ڵ�G����AG=
BC=
��
��Rt��AGP1��cos��P1AG=
=
=
��
���P1AG=30�㣬
���P1AB=45��-30��=15�㣻
ͬ����ã���P2AG=30�㣬��P2AB=45��+30��=75�㣮
���PAB�Ķ���Ϊ15���75�㣮
̽��������AMN���ܳ���������Сֵ��
���ͼ3��ʾ������AD��

�ߡ�ABCΪ����ֱ�������Σ���DΪб��BC���е㣬
��AD=CD����C=��MAD=45�㣮
�ߡ�EDF=90�㣬��ADC=90�㣬
���MDA=��NDC��
���ڡ�AMD���CND�У�
���AMD�ա�CND��ASA����
��AM=CN��
��AM=x����CN=x��AN=AC-CN=
BC-CN=
-x��
��Rt��AMN�У��ɹ��ɶ����ã�
MN=
=
=
=
��
��AMN���ܳ�Ϊ��AM+AN+MN=
+
��
��x=
ʱ������Сֵ����СֵΪ
+
=
��
���AMN�ܳ�����СֵΪ
��

�����⣬�á�CFB=60�㣬FPΪ��ƽ���ߣ����CFP=30�㣬
��CF=BC•tan30��=3��
| ||
| 3 |
| 3 |
��CP=CF•tan��CFP=
| 3 |
| ||
| 3 |
����A��AG��BC�ڵ�G����AG=
| 1 |
| 2 |
| 3 |
| 2 |
��PG=CG-CP=
| 3 |
| 2 |
| 1 |
| 2 |
��Rt��APG�У��ɹ��ɶ����ã�
AP=
| AG2+PG2 |
(
|
| ||
| 2 |
��2���ɣ�1����֪��FC=
| 3 |
���ͼ2��ʾ���Ե�AΪԲ�ģ���FC=
| 3 |
| 3 |

����A��AG��BC�ڵ�G����AG=
| 1 |
| 2 |
| 3 |
| 2 |
��Rt��AGP1��cos��P1AG=
| AG |
| AP1 |
| ||
|
| ||
| 2 |
���P1AG=30�㣬
���P1AB=45��-30��=15�㣻
ͬ����ã���P2AG=30�㣬��P2AB=45��+30��=75�㣮
���PAB�Ķ���Ϊ15���75�㣮
̽��������AMN���ܳ���������Сֵ��
���ͼ3��ʾ������AD��

�ߡ�ABCΪ����ֱ�������Σ���DΪб��BC���е㣬
��AD=CD����C=��MAD=45�㣮
�ߡ�EDF=90�㣬��ADC=90�㣬
���MDA=��NDC��
���ڡ�AMD���CND�У�
|
���AMD�ա�CND��ASA����
��AM=CN��
��AM=x����CN=x��AN=AC-CN=
| ||
| 2 |
3
| ||
| 2 |
��Rt��AMN�У��ɹ��ɶ����ã�
MN=
| AM2+AN2 |
x2+(
|
2x2-3
|
2(x-
|
��AMN���ܳ�Ϊ��AM+AN+MN=
3
| ||
| 2 |
2(x-
|
��x=
3
| ||
| 4 |
3
| ||
| 2 |
|
3+3
| ||
| 2 |
���AMN�ܳ�����СֵΪ
3+3
| ||
| 2 |
�����������Ǽ����ۺ��⣬�����˽�ֱ�������Ρ����ɶ�����ȫ�������Ρ����κ�����ֵ��֪ʶ�㣮�ѵ����ڵڣ�3���ʣ��ɷ��ֲ�֤����AMD�ա�CNDȡ�ý����ͻ�Ƶ㣬�����ù��ɶ����Ͷ��κ��������������Сֵ��

��ϰ��ϵ�д�
 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
�����Ŀ
 ��2013•÷�ݣ���ͼ����֪������y=2x2-2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��2013•÷�ݣ���ͼ����֪������y=2x2-2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��