题目内容
当a满足________时无论x为何值,分式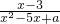 总有意义.
总有意义.
a>
分析:由于无论x为何值,分式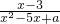 总有意义,则x2-5x+a≠0时,即x2-5x+a=0无实数根,然后利用根的判别式的意义得到a的不等式,解不等式即可.
总有意义,则x2-5x+a≠0时,即x2-5x+a=0无实数根,然后利用根的判别式的意义得到a的不等式,解不等式即可.
解答:根据题意得,∵x2-5x+a≠0时,原分式总有意义,
∴△<0,即52-4a<0,解得a> .
.
故答案为a> .
.
点评:本题考查了分式有意义的条件:当分式的分母不为零时,分式有意义.也考查了一元二次方程根的判别式的使用.

分析:由于无论x为何值,分式
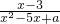 总有意义,则x2-5x+a≠0时,即x2-5x+a=0无实数根,然后利用根的判别式的意义得到a的不等式,解不等式即可.
总有意义,则x2-5x+a≠0时,即x2-5x+a=0无实数根,然后利用根的判别式的意义得到a的不等式,解不等式即可.解答:根据题意得,∵x2-5x+a≠0时,原分式总有意义,
∴△<0,即52-4a<0,解得a>
 .
.故答案为a>
 .
.点评:本题考查了分式有意义的条件:当分式的分母不为零时,分式有意义.也考查了一元二次方程根的判别式的使用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

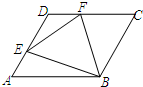 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.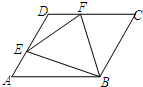 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.