题目内容
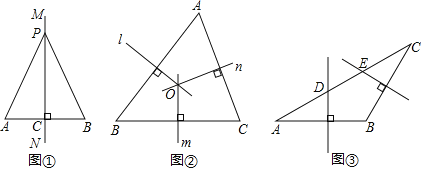
【题目】如图1,在正方形ABCD中,点O是对角线BD的中点.
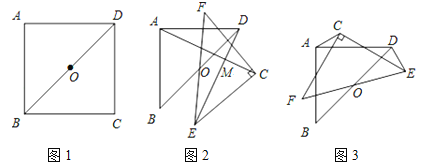
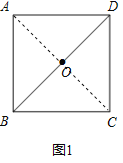
(1)观察猜想:将图1中的△BCD绕点O逆时针旋转至图2中△ECF的位置,连接AC,DE,则线段AC与DE的数量关系是 ,直线AC与DE的位置关系是 .
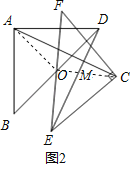
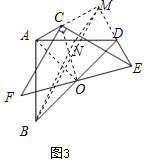
(2)类比探究:将图2中的△ECF绕点O逆时针旋转至图3的位置,(1)中的结论是否成立?并说明理由.
(3)拓展延伸:将图2中的△ECF在平面内旋转,设直线AC与DE的交点为M,若AB=4,请直接写出BM的最大值与最小值.
【答案】(1)AC=DE,AC⊥DE;(2)(1)中的结论:AC=DE,AC⊥DE仍然成立,见解析;(3)BM的最大值为![]() ﹣2,最小值为
﹣2,最小值为![]() +2.
+2.
【解析】
(1)连接OA,OC,可证△AOC≌△DOE(SAS);
(2)方法和(1)相同,易证△AOC≌△DOE(SAS);
(3)在旋转过程中,取AD中点N,连接MN,BN,BM,BM、MN、BN不共线时构成三角形,由三角形边的关系“三角形中两边之和大于第三边,两边之差小于第三边”可知:BN﹣MN<BM<BN+MN,当B,N,M共线时,
得到BM=BN+MN和BM=BN﹣MN分别为BN的最大值、最小值.
(1)如图1和图2,连接OA,OC,
∵正方形ABCD,
∴AB=BC=CD=AD,OA=OB=OC=OD,∠AOD=∠COE=90°,
∴∠AOD+∠DOC=∠COE+∠DOC,即∠AOC=∠DOE,
∴△AOC≌△DOE(SAS),
∴AC=DE,∠ACO=∠DEO,
∵∠DEO+∠EMO=90°,∠EMO=∠CMD,
∴∠ACO+∠CMD=90°,
∴AC⊥DE,
故答案为:AC=DE,AC⊥DE;
(2)(1)中的结论:AC=DE,AC⊥DE仍然成立,
如图3,连接OA,OC,延长AC,ED交于M,
∵∠AOC+∠COD=∠DOE+∠COD=90°,
∴∠AOC=∠DOE,
∵OA=OC=OD=OE,
∴△AOC≌△DOE(SAS),
∴∠OAC=∠=OCA=∠ODE=∠OED,
∵∠AOC+∠OAC+∠OCA=180°,
∴∠AOC+∠OAC+∠OED=180°,
∴∠OAC+∠AOE+∠OED=270°,
∵∠OAC+∠AOE+∠OED+∠M=360°,
∴∠M=90°,
∴AC⊥DE;
(3)如图3,取AD中点N,连接MN,BN,BM,
AB=AD=4,
在Rt△AMD中,∠AMD=90°,AN=DN,∴MN=![]() AD=
AD=![]() ×4=2,
×4=2,
在Rt△ABN中,BN=![]() ,
,
当△ECF在平面内旋转时,BN﹣MN≤BM≤BN+MN,
∴2![]() ﹣2≤BM≤2
﹣2≤BM≤2![]() +2.
+2.
∴BM的最大值为2![]() ﹣2,最小值为2
﹣2,最小值为2![]() +2.
+2.

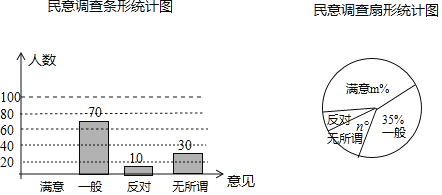
【题目】某校举行了创建全国文明城市知识竞赛活动,初一年级全体同学参加了竞赛.收集数据:现随机抽取初一年级30名同学“创文知识竞赛”成绩,分数如下(单位:分):
90 | 85 | 68 | 92 | 81 | 84 | 95 | 93 | 87 | 89 | 78 | 99 | 89 | 85 | 97 |
88 | 81 | 95 | 86 | 98 | 95 | 93 | 89 | 86 | 84 | 87 | 79 | 85 | 89 | 82 |
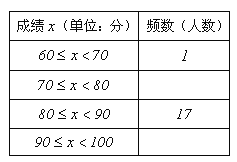

⑴请将图表中空缺的部分补充完整;
⑵学校决定表彰“创文知识竞赛”成绩在90分以上的同学,根据上表统计结果估计该校初一年级360人中,约有多少人将获得表彰;
⑶“创文知识竞赛”中,受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有恐龙图案的概率是 .
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
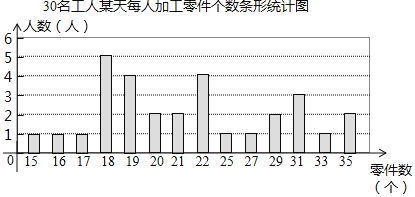
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.