题目内容
如图，在平行四边形ABCD中，E、F分别是边AD、BC的中点，AC 分别交BE、DF于点M、N，给出下列结论：①△ABM≌△CDN；②AM=
AC； ③DN=2NF；④S△AMB =
S△ABC，其中正确的是 （只填序号）
AC； ③DN=2NF；④S△AMB = S△ABC，其中正确的是 （只填序号）①②③
在?ABCD中，AD∥BC，AD=BC，
又E、F分别是边AD、BC的中点，
∴BF∥DE，BF=DE，
∴四边形BFDE是平行四边形，
∴BE∥DF，
∴∠AMB=∠ANF=∠DNC，
∵∠BAM=∠DCN，AB=CD，
∴△ABM≌△CDN；
E是AD的中点，BE∥DF，
∴M是AN的中点，
同理N是CM的中点，
∴AM="1/3" AC；
DN=BM=2NF；
S△AMB=1/2S△ABC不成立．故答案为：①②③．
又E、F分别是边AD、BC的中点，
∴BF∥DE，BF=DE，
∴四边形BFDE是平行四边形，
∴BE∥DF，
∴∠AMB=∠ANF=∠DNC，
∵∠BAM=∠DCN，AB=CD，
∴△ABM≌△CDN；
E是AD的中点，BE∥DF，
∴M是AN的中点，
同理N是CM的中点，
∴AM="1/3" AC；
DN=BM=2NF；
S△AMB=1/2S△ABC不成立．故答案为：①②③．
练习册系列答案
天天练口算系列答案
相关题目
-
-
-4.
-
.
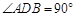，CA = 10，DB = 6，OE⊥AC于点O，连结CE，则△CBE的周长是_________．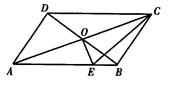
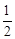CD，CF=
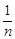CD，CF=
