题目内容
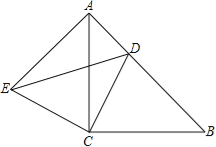
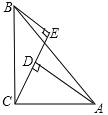
【题目】如图所示,已知在△ABC中,∠C=90°,AC=5,AB=13.点D在边AC上,且点D到边AB和边BC的距离相等.
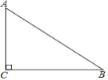
(1)用直尺圆规作出点D(不写作法,保留作图痕迹,在图上标注清楚点D);
(2)求△ABD的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)作∠ABC的角平分线交AC于D,则根据角平分线的性质可判断点D到边AB和边BC的距离相等;
(2)过点D作DE⊥AB于E,如图,利用勾股定理计算出BC=12,设DE=x,则DC=x,利用S△ADB+S△BCD=S△ABC得到![]() x13+
x13+![]() x12=
x12=![]() 125,然后解方程求出x即可.
125,然后解方程求出x即可.
(1)如图,点D就是所要求作的点;
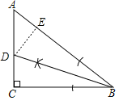
(2)过点D作DE⊥AB于E,如图,
在Rt△ABC中,BC=![]() =12,
=12,
设DE=x,则DC=x,
∵S△ADB+S△BCD=S△ABC,
∴![]() x13+
x13+![]() x12=
x12=![]() 125,
125,
∴x=![]() ,
,
∴S△ADB=![]() ABDE=
ABDE=![]() ×13×
×13×![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
图书种类 | 频数 | 频率 |
科普常识 | 840 | B |
名人传记 | 816 | 0.34 |
漫画丛书 | A | 0.25 |
其它 | 144 | 0.06 |
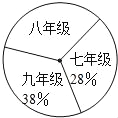
(1)求该校八年级的人数占全校总人数的百分率.
(2)求表中A,B的值.
(3)该校学生平均每人读多少本课外书?