题目内容
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.
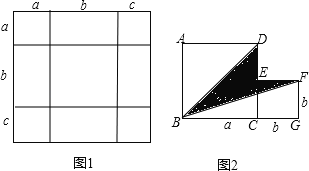
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
【答案】(1)a2+b2+c2+2ab+2bc+2ac;(2)20
【解析】
试题分析:(1)此题根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积,种是大正方形的面积,可得等式
(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
(2)利用S阴影=正方形ABCD的面积+正方形ECGF的面积﹣三角形BGF的面积﹣三角形ABD的面积求解.
解(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac
(2)∵a+b=10,ab=20,
∴S阴影=a2+b2﹣![]() (a+b)×b﹣
(a+b)×b﹣![]() a2=
a2=![]() a2+
a2+![]() b2﹣
b2﹣![]() ab=
ab=![]() (a+b)2﹣
(a+b)2﹣![]() ab=
ab=![]() ×102﹣
×102﹣![]() ×20=50﹣30=20.
×20=50﹣30=20.

练习册系列答案
相关题目