题目内容
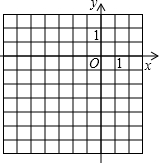 在同一平面直角坐标系中有6个点:A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(-2,-3),F(0,-4).
在同一平面直角坐标系中有6个点:A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(-2,-3),F(0,-4).(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)若将直线EF沿y轴向上平移,当它经过点D时,设此时的直线为l1.
①判断直线l1与⊙P的位置关系,并说明理由;
②再将直线l1绕点D按顺时针方向旋转,当它经过点C时,设此时的直线为l2.求直线l2与⊙P的劣弧CD围成的图形的面积.(结果保留π)
分析:(1)判断点与圆的位置关系,可以比较圆的半径与点到圆心的距离的大小关系;
(2)①判断直线与圆的位置关系,即是比较圆的半径与点到直线的距离的大小关系;
②根据扇形的面积公式就可以求出面积.
(2)①判断直线与圆的位置关系,即是比较圆的半径与点到直线的距离的大小关系;
②根据扇形的面积公式就可以求出面积.
解答: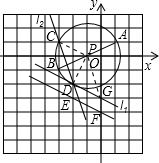 解:(1)所画⊙P如图所示,
解:(1)所画⊙P如图所示,
由图可知⊙P的半径为
,而PD=
.
∴点D在⊙P上.
(2)①∵直线EF向上平移1个单位经过点D,且经过点G(0,-3),
∴PG2=12+32=10,PD2=5,DG2=5.
∴PG2=PD2+DG2.
则∠PDG=90°,
∴PD⊥l1.
∴直线l1与⊙P相切.
②∵PC=PD=
,CD=
,
∴PC2+PD2=CD2.
∴∠CPD=90度.
∴S扇形=
=
π,S△PCD=
(
)2=
.
∴直线l2与劣弧CD围成的图形的面积为
-
.
 解:(1)所画⊙P如图所示,
解:(1)所画⊙P如图所示,由图可知⊙P的半径为
| 5 |
| 5 |
∴点D在⊙P上.
(2)①∵直线EF向上平移1个单位经过点D,且经过点G(0,-3),
∴PG2=12+32=10,PD2=5,DG2=5.
∴PG2=PD2+DG2.
则∠PDG=90°,
∴PD⊥l1.
∴直线l1与⊙P相切.
②∵PC=PD=
| 5 |
| 10 |
∴PC2+PD2=CD2.
∴∠CPD=90度.
∴S扇形=
(
| ||
| 4 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 5 |
| 2 |
∴直线l2与劣弧CD围成的图形的面积为
| 5π |
| 4 |
| 5 |
| 2 |
点评:本题主要考查了点与圆的位置关系以及直线与圆的位置关系的判断方法;扇形的面积计算方法.

练习册系列答案
相关题目


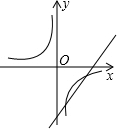
 直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )
直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )