Question

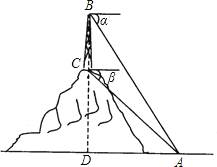
【题目】如图，在山顶上有一座电视塔，在塔顶B处，测得地面上一点A的俯角α=60°，在塔底C处测得的俯角β=45°，已知BC=60m，求山高CD（精确到1m，≈1.732）

Answer 1

【答案】山高CD约为82米．

【解析】

试题分析：首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形△DBA、△ADC，应利用其公共边AD构造等量关系，借助BC=DB﹣DC构造方程关系式，进而可求出答案．

解：设山高CD=x（米），

∵∠CAD=∠β=45°，∠BAD=∠α=60°，∠ADB=90°，

∴AD=CD=x，BD=ADtan60°=x．

∵BD﹣CD=BC=60，

∴x﹣x=60．

∴x==30（+1）．

∴CD=30×（1.732+1）≈82（米）．

答：山高CD约为82米．