题目内容
【题目】在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.
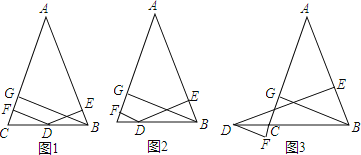
(1)、如图1,若D是BC边上的中点,∠A=45°,DF=3,求AC的长;
(2)、如图2,D是线段BC上的任意一点,求证:BG=DE+DF;
(3)、在图3,D是线段BC延长线上的点,猜想DE、DF与BG的关系,并证明.
【答案】(1)、AC=6![]() ;(2)、证明过程见解析;(3)、DE﹣DF=BG;证明过程见解析.
;(2)、证明过程见解析;(3)、DE﹣DF=BG;证明过程见解析.
【解析】
试题分析:(1)、连结AD,根据△ABC的面积=△ABD的面积+△ACD的面积得出BG=DE+DF,根据角平分线的性质得出BG=6,根据等腰直角三角形的性质得出AC的长度;(2)、连结AD,根据△ABC的面积=△ABD的面积+△ACD的面积得出线段之间的关系;(3)、连结AD,根据△ABC的面积=△ABD的面积+△ACD的面积得出线段之间的关系.
试题解析:(1)、如图1,连结AD.则△ABC的面积=△ABD的面积+△ACD的面积,
即![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() ACBG, ∵AB=AC,∴DE+DF=BG, ∵D是BC边上的中点,∴AD平分∠BAC,
ACBG, ∵AB=AC,∴DE+DF=BG, ∵D是BC边上的中点,∴AD平分∠BAC,
∴DE=DF=3,∴BG=6, ∵∠A=45°,∴△AGB是等腰直角三角形, ∴AB=![]() BG=6
BG=6![]() ,∴AC=6
,∴AC=6![]() ;
;
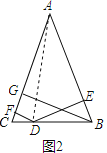
(2)、如图2,连结AD.则△ABC的面积=△ABD的面积+△ACD的面积,
即![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() ACBG, ∵AB=AC,∴DE+DF=BG;
ACBG, ∵AB=AC,∴DE+DF=BG;
(3)、DE﹣DF=BG,
如图3,连接AD,则△ABC的面积=△ABD的面积﹣△ACD的面积, 即![]() ABDE﹣
ABDE﹣![]() ACDF=
ACDF=![]() ACBG,
ACBG,
∵AB=AC,∴DE﹣DF=BG.



练习册系列答案
相关题目