题目内容
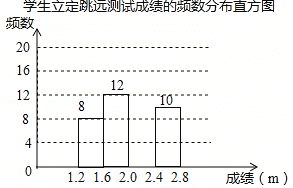
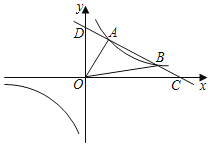
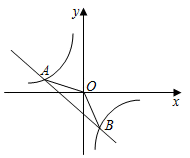
【题目】如图，一次函数y＝﹣x+b的图象与反比例函数y＝
的图象交于A、B两点，且A点坐标为（﹣2，1），一次函数交x轴于点C．
（1）试确定上述反比例函数和一次函数的表达式；
（2）求△AOB的面积；
（3）直接写出使反比例函数大于一次函数的x的取值范围．
【答案】（1）反比例函数解析式为y＝﹣
，一次函数解析式为y＝﹣x﹣1；（2）
；（3）﹣2＜x＜0或x＞1
【解析】
（1）把A(﹣2，1)代入y＝﹣x+b中，求出b，得到一次函数解析式；然后把A(﹣2，1)代入y＝
中，求出m，得到反比例函数解析式；
（2）先求出直线y＝﹣x﹣1与y轴的交点坐标，再联立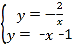
，求出点B的坐标，然后利用三角形面积公式计算△AOB的面积，即可；
（3）结合图象写出反比例函数图象在一次函数图象上方对应的自变量的范围即可．
（1）把A(﹣2，1)代入y＝﹣x+b，得2+b＝1，解得：b＝﹣1，
∴一次函数解析式为：y＝﹣x﹣1；
把A(﹣2，1)代入y＝，得：m＝﹣2×1＝﹣2，
∴反比例函数解析式为：y＝﹣；
（2）当x＝0时，y＝﹣x﹣1＝﹣1，则直线y＝﹣x﹣1与y轴的交点坐标为(0，﹣1)，
联立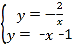，得：﹣＝﹣x﹣1，
解得：
，
∴B(1，-2)，
∴△AOB的面积＝
×1×（2+1）＝；
（3）根据函数图象，反比例函数图象在一次函数图象上方所对应的自变量的范围是：﹣2＜x＜0或x＞1．
小学生10分钟口算测试100分系列答案
【题目】为了更好的治理西流湖水质，保护环境，市治污公司决定购买 10 台污水处理设备．现有 A、B 两种型号的设备，其中每台的价格，月处理污水量如下表：
A 型 | B 型 | |
价格（万元/台） | a | b |
处理污水量（吨／月） | 240 | 200 |
经调查：购买一台 A 型设备比购买一台 B 型设备多 2 万元，购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元．
（1）求 a，b 的值；
（2）经预算：市治污公司购买污水处理设备的资金不超过 105 万元，你认为该公司 有哪几种购买方案；
（3）在（2）问的条件下，若每月要求处理西流湖的污水量不低于 2040 吨，为了节 约资金，请你为治污公司设计一种最省钱的购买方案．
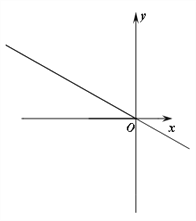
【题目】参照学习函数的过程方法，探究函数
的图像与性质，因为
，即
，所以我们对比函数
来探究列表：
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 |
|
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点：在平面直角坐标系中以自变量
的取值为横坐标，以
相应的函数值为纵坐标，描出相应的点如图所示：
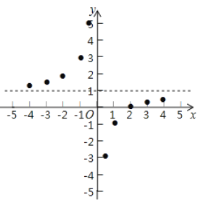
（1）请把
轴左边各点和右边各点分别用一条光滑曲线，顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当
时，随的增大而______；（“增大”或“减小”）
②的图象是由
的图象向______平移______个单位而得到的；
③图象关于点______中心对称.（填点的坐标）
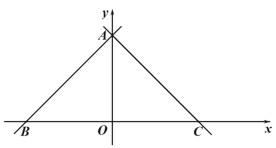
（3）函数与直线
交于点
，
，求
的面积.
