题目内容
【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M沿路线O→A→C运动．
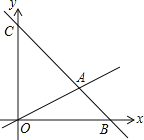
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）当△OMC的面积是△OAC的面积的
时，求出这时点M的坐标．
【答案】（1）y=﹣x+6；（2）12；（3）M1（1，
）或M2（1，5）．
【解析】
试题分析：（1）利用待定系数法即可求得函数的解析式；
（2）求得C的坐标，即OC的长，利用三角形的面积公式即可求解；
（3）当△OMC的面积是△OAC的面积的
时，根据面积公式即可求得M的横坐标，然后代入解析式即可求得M的坐标．
解：（1）设直线AB的解析式是y=kx+b，
根据题意得：
，
解得：
，
则直线的解析式是：y=﹣x+6；
（2）在y=﹣x+6中，令x=0，解得：y=6，
S△OAC=
×6×4=12；
（3）设OA的解析式是y=mx，则4m=2，
解得：m=，
则直线的解析式是：y=x，
∵当△OMC的面积是△OAC的面积的
时，
∴M的横坐标是×4=1，
在y=x中，当x=1时，y=，则M的坐标是（1，）；
在y=﹣x+6中，x=1则y=5，则M的坐标是（1，5）．
则M的坐标是：M1（1，）或M2（1，5）．
练习册系列答案
相关题目
【题目】七年级学生完成课题学习“从数据谈节水”后，积极践行“节约用水，从我做起”，现在从七年级400名学生中选出10名学生统计各自家庭一个月的节水情况如下表：
节水量（m3） | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
家庭数 | 1 | 2 | 2 | 4 | 1 |
那么这组数据的众数和平均数分别是（ ）
A. 0.4m3和0.34m3 B. 0.4m3和0.3m3 C. 0.25m3和0.34m3 D. 0.25m3和0.3m3
