题目内容
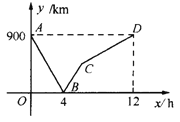
【题目】一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．根据图象进行以下探究：
信息读取：(1)甲、乙两地之间的距离为
(2)请解释图中点B的实际意义；
(3)求慢车和快车的速度；
(4)求线段BC所表示的y与x之间的函数关系式，并写出自变量x的取值范围；
(5)若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同，在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？。
【答案】（1）900；（2）当慢车行驶4h时，慢车和快车相遇．（3）
；150km/h．（4）
；自变量
的取值范围是
．（5）0.75h．
【解析】（1）明确实际意义，原点的表示的含义。甲、乙两地之间的距离为600千米。
（2）根据实际意义：此时两车距离为0所以表示的是两车相遇。
（3）从图上看甲乙两车行驶完600千米共用时2小时，而动车由甲地到乙地共用时为了6小时。所以动车速度为：600÷6=100千米/小时。而快车速度为：600÷2-100=200千米/小时。
（4）C点表示的实际意义为快车恰好到站，此时用时为600÷200=3小时。而从相遇到快车到站共用时为3-2=1小时，此时两车背向而行，所以相距为（100+200）×1=300千米
所以可得点B、C两点坐标为（2，0）、（3，300）。此时把两点代入y=kx+b可得y=300x—600 (2≤x≤3) 。
（5）1/3×300÷200="1/2"
答：晚出发半小时.
练习册系列答案
相关题目
