题目内容
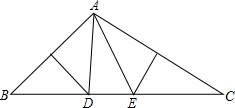
如图，有一底角为35°的等腰△ABC，两腰AB、AC的垂直平分线与底边分别相交于D、E，则∠DAE的度数是______．
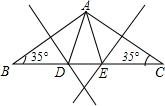
∵两腰AB、AC的垂直平分线与底边分别相交于D、E，
∴BD=AD，CE=AE，
∴∠DAB=∠B=35°，∠C=∠EAC=35°，
∵∠B=∠C=35°，
∴∠BAC=180°-∠B-∠C=110°，
∴∠DAE=110°-35°-35°=40°，
故答案为：40°．
∴BD=AD，CE=AE，
∴∠DAB=∠B=35°，∠C=∠EAC=35°，
∵∠B=∠C=35°，
∴∠BAC=180°-∠B-∠C=110°，
∴∠DAE=110°-35°-35°=40°，
故答案为：40°．
练习册系列答案
学业测评一课一测系列答案
相关题目
