题目内容
若A、B为锐角,且|sinA- |+
|+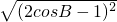 =0,则∠A+∠B=________度.
=0,则∠A+∠B=________度.
120
分析:根据非负数的性质得出sinA- =0,
=0,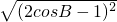 =0,求出∠A、∠B的值.
=0,求出∠A、∠B的值.
解答:∵|sinA- |+
|+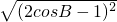 =0,
=0,
∴sinA- =0,
=0,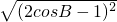 =0,
=0,
∴sinA= ;2cosB-1=0,cosB=
;2cosB-1=0,cosB= ,
,
∴∠A=60°,∠B=60°,
∴∠A+∠B=60°+60°=120°.
点评:本题考查特殊角的三角函数值和非负数的性质.
两个非负数相加,和为0,则这两个非负数的值均为0.
分析:根据非负数的性质得出sinA-
 =0,
=0,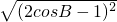 =0,求出∠A、∠B的值.
=0,求出∠A、∠B的值.解答:∵|sinA-
 |+
|+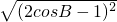 =0,
=0,∴sinA-
 =0,
=0,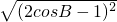 =0,
=0,∴sinA=
 ;2cosB-1=0,cosB=
;2cosB-1=0,cosB= ,
,∴∠A=60°,∠B=60°,
∴∠A+∠B=60°+60°=120°.
点评:本题考查特殊角的三角函数值和非负数的性质.
两个非负数相加,和为0,则这两个非负数的值均为0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 |+
|+ =0,则∠A+∠B= 度.
=0,则∠A+∠B= 度.