题目内容
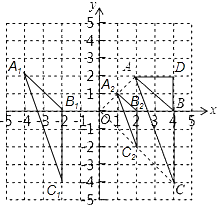
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4). (Ⅰ)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(Ⅱ)以点O为位似中心,将△ABC缩小为原来的 ![]() ,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.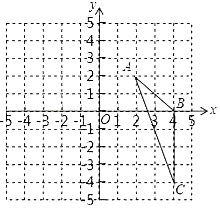
【答案】解:(Ⅰ)如图所示:△A1B1C1 , 即为所求; (Ⅱ)如图所示:△A2B2C2 , 即为所求,
由图形可知,∠A2C2B2=∠ACB,
过点A作AD⊥BC交BC的延长线于点D,
由A(2,2),C(4,﹣4),B(4,0),易得D(4,2),
故AD=2,CD=6,AC= ![]() =2
=2 ![]() ,
,
∴sin∠ACB= ![]() =
= ![]() =
= ![]() ,
,
即sin∠A2C2B2= ![]() .
.
【解析】(Ⅰ)直接利用平移的性质得出对应点位置进而得出答案; (Ⅱ)利用位似图形的性质得出对应点位置,再利用锐角三角三角函数关系得出答案.

练习册系列答案
相关题目