题目内容
【题目】如图,在ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则 ![]() 的长为 .
的长为 . 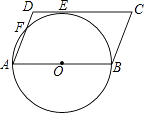
【答案】π
【解析】解:如图连接OE、OF, 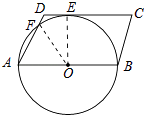
∵CD是⊙O的切线,
∴OE⊥CD,
∴∠OED=90°,
∵四边形ABCD是平行四边形,∠C=60°,
∴∠A=∠C=60°,∠D=120°,
∵OA=OF,
∴∠A=∠OFA=60°,
∴∠DFO=120°,
∴∠EOF=360°﹣∠D﹣∠DFO﹣∠DEO=30°,![]() 的长=
的长= ![]() =π.
=π.
所以答案是:π.
【考点精析】掌握平行四边形的性质和切线的性质定理是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?