Question

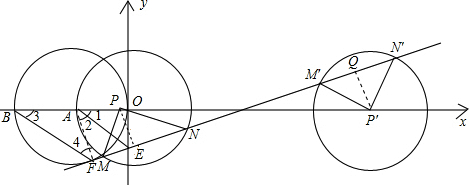
如图，已知A（-1，0），E（0，-

2

2

），以点A为圆心，以AO长为半径的圆交x轴于另一点B，过点B作BF∥AE交⊙A于点F，直线FE交x轴于点C．
（1）求证：直线FC是⊙A的切线；
（2）求点C的坐标及直线FC的解析式；
（3）有一个半径与⊙A的半径相等，且圆心在x轴上运动的⊙P．若⊙P与直线FC相交于M，N两点，是否存在这样的点P，使△PMN是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

（1）证明：连接AF，
∵AE∥BF，
∴∠1=∠3，∠4=∠2，
又∵AB=AF，
∴∠3=∠4，
∴∠1=∠2，
又∵AO=AF，AE=AE，
∴△AOE≌△AFE，
∴∠AFE=∠AOE=90°，
∴FC是⊙O的切线．

（2）方法①由（1）知EF=OE=

2

2

，
∵AE∥BF，
∴

AC

AB

=

CE

EF

，
∴

OC+1

1

=

CE

2 2

，
∴CE=

2

2

CO+

2

2

①；
又∵OE²+OC²=CE²，
∴CE²=（

2

2

）²+CO²②；
由①②解得OC=0（舍去）或OC=2，
∴C（2，0），
∵直线FC经过E（0，-

2

2

），C（2，0）两点，
设FC的解析式：y=kx+b，
∴

2k+b=0 b=- 2 2

，
解得

k= 2 4 b=- 2 2

，
∴直线FC的解析式为y=

2

4

x-

2

2

．
方法②：
∵CF切⊙A于点F，
∴∠AFC=∠EOC=90°，
又∠ACF=∠OCE，
∴△COE∽△CFA，
∴

OE

AF

=

CO

CF

，
∴

2 2

1

=

CO

CE+ 2 2

，
即CE=

2

CO-

2

2

①；
又OE²+OC²=CE²，
∴CE²=（

2

2

）²+CO²②；
由①②解得CO=0（舍去）或CO=2；
∴C（2，0）
（求FC的解析式同上）．
方法③∵AE∥BF，
∴

AC

AB

=

CE

EF

，
∴

OC+1

1

=

CE

2 2

，
∴CE=

2

2

CO+

2

2

①，
∵FC切⊙A于点F，
∴∠AFC=∠COE=90°，
∴∠ACE=∠OCE，
∴△COE∽△CFA，
∴

OE

AF

=

CO

CF

，
∴

2 2

1

=

CO

CE+ 2 2

，
∴CE=

2

CO-

2

2

②．
由①②解得：CO=2，
∴C（2，0），
（求FC的解析式同上）．

（3）存在：
当点P在点C左侧时，若∠MPN=90°，过点P作PE⊥MN于点E，
∵∠MPN=90°，PM=PN，
∴PE=PM×cos45°⁼

2

2

，
∵AF⊥FC，
∴PE∥AF，
∴△CPE∽△CAF，
∴

PE

AF

=

CP

CA

，
∴

2 2

1

=

CP

3

，
∴CP=

3 2

2

，
∴PO=

3 2

2

-2，
∴P（2-

3 2

2

，0）．
当点P在点C右侧P′时，设∠M′P′N′=90°，过点P′作P′Q⊥M′N′于点Q，则P′Q=

2

2

．
∴P′Q=PE，可知P′与P关于点C中心对称，根据对称性得：
∴OP′=OC+CP′=2+

3 2

2

，
∴P′（2+

3 2

2

，0），
∴存在这样的点P，使得△PMN为直角三角形，P点坐标（2-

3 2

2

，0）或（2+

3 2

2

，0）．