题目内容
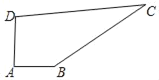
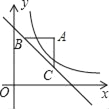
【题目】如图,在四边形 ABCD 中, ABC 90, CD AD , BE AD , AD2 CD2 2 AB2,若四边形 ABCD 的面积为18,则 BE 的长为_____.

【答案】![]()
【解析】
连接AC,过B点作BF ⊥DF,交DC的延长线于点F,利用勾股定理与题意可证AB=BC,再通过“角边角”证明△ABE≌△CBF,进而得到四边形BEDF为正方形,然后通过正方形的面积公式即可得解.
解:如图:连接AC,过B点作BF ⊥DF,交DC的延长线于点F,
∵∠ABC=90°,
∴AB2+BC2=AC2,
∵CD⊥AD,
∴AD2+CD2=AC2,
又∵AD2 CD2 2 AB2,
∴AB2+BC2=2 AB2,
∴AB=BC,
∵∠ABE+∠EBC=90°,∠CBF+∠EBC=90°,
∴∠ABE=∠CBF,
∵∠AEB=∠CFB=90°,
∴△ABE≌△CBF(ASA),
∴BE=BF,
∴四边形BEDF为正方形,
∵S四边形ABCD=S正方形BEDF=18,
∴BE=![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目