题目内容
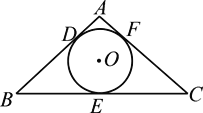
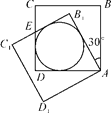
【题目】将正方形ABCD绕点A按逆时针方向旋转30°，得正方形AB1C1D1，B1C1交CD于点E，AB＝
，则四边形AB1ED的内切圆半径为_________
【答案】
【解析】
首先作∠DAF与∠AB1C1的角平分线，交于点O，则O为该圆的圆心，过O作OF⊥AB1交AB1于点F，则OF即为所求，根据角平分线的性质可得∠OAF=30°，∠AB1O=45°，根据等腰三角形的性质以及含30°角的直角三角形性质可得B1F=x，AF=
-x，接下来在Rt△OFA，利用勾股定理即可得到关于x的方程，解方程即可求解.
作∠DAF与∠AB1C1的角平分线，交于点O，过O作OF⊥AB1交AB1于点F，
AB=AB1=，∠BAB1=30°，
∵四边形AB1C1D1是正方形，∠DAF与∠AB1C1的角平分线交于点O，∠BAB1=30°
∴∠OAF=30°，∠AB1O=45°
∵OF⊥AB1
∴B1F=OF=
OA
设B1F=x，则AF=-x
∴（-x）2+x2=（2x）2
解得x=或x=
（舍去）
即四边AB1ED的内切圆的半径为.
故答案为：.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
