题目内容
【题目】已知抛物线y=x2+bx+3经过点A(﹣1,8),顶点为M;
(1)求抛物线的表达式;
(2)设抛物线对称轴与x轴交于点B,连接AB、AM,求△ABM的面积.
【答案】(1)y=x2﹣4x+3;(2)![]() .
.
【解析】
(1)把点A的坐标代入函数解析式,列出关于系数b的方程,通过解方程求得b的值即可;
(2)由(1)中函数解析式得到对称轴为x=2,然后结合三角形的面积公式进行解答即可.
解:(1)∵抛物线y=x2+bx+3经过点A(﹣1,8),
∴8=(-1)2﹣b+3,
解得b=﹣4,
∴所求抛物线的表达式为y=x2﹣4x+3;
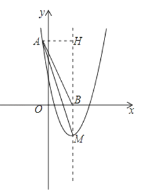
(2)作AH⊥BM于点H,
∵由抛物线y=x2﹣4x+3解析式可得,
点M的坐标为(2,﹣1),点B的坐标为(2,0),
∴BM=1,
∵对称轴为直线x=2,
∴AH=3,
∴△ABM的面积![]() .
.
故答案为:(1)y=x2﹣4x+3;(2)![]() .
.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目