题目内容
【题目】如图，将一张矩形大铁皮切割成九块，切痕如下图虚线所示，其中有两块是边长都为mcm的大正方形，两块是边长都为ncm的小正方形，五块是长宽分别是mcm、ncm的全等小矩形，且m＞n．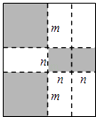 
（1）用含m、n的代数式表示切痕的总长为cm；
（2）若每块小矩形的面积为48cm2 ， 四个正方形的面积和为200cm2 ， 试求该矩形大铁皮的周长．
【答案】
（1）6m+6n
（2）解：由题意得：mn=48，2m2+2n2=200，
∴m2+n2=100，
∴（m+n）2=m2+n2+2mn=196，
∵m+n＞0，
∴m+n=14，
∴周长=2（m+2n+2m+n）=6m+6n=6（m+n）=84
【解析】解：（1）切痕总长=2[（m+2n）+（2m+n）]， =2（m+2n+2m+n），
=6m+6n；
所以答案是：6m+6n；
练习册系列答案
阅读快车系列答案
相关题目
