题目内容
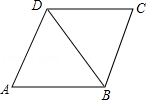
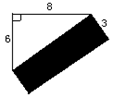
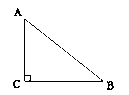
一块木板如图所示,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,木板的面积为
| A.60 | B.30 | C.24 | D.12 |
C
本题考查正确运用勾股定理.连接AC,利用勾股定理解出直角三角形ABC的斜边,通过三角形ACD的三边关系可确定它为直角三角形,木板面积为这两三角形面积之差
解:连接AC,
∵在△ABC中,AB=4,BC=3,∠B=90°,
∴AC=5,
∵在△ACD中,AC=5,DC=12,AD=13,
∴DC2+AC2=122+52=169,AD2=132=169,∴DC2+AC2=AD2,△ACD为直角三角形,AD为斜边,
∴木板的面积为:S△ACD-S△ABC=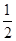 ×5×12-
×5×12-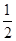 ×3×4=24.
×3×4=24.
故选C.
解:连接AC,
∵在△ABC中,AB=4,BC=3,∠B=90°,
∴AC=5,
∵在△ACD中,AC=5,DC=12,AD=13,
∴DC2+AC2=122+52=169,AD2=132=169,∴DC2+AC2=AD2,△ACD为直角三角形,AD为斜边,
∴木板的面积为:S△ACD-S△ABC=
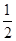 ×5×12-
×5×12-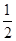 ×3×4=24.
×3×4=24.故选C.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
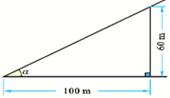
 ,则菱形ABCD的面积为 cm2.
,则菱形ABCD的面积为 cm2.