题目内容
(2013•眉山)我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
(1)李老师采取的调查方式是
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要在抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
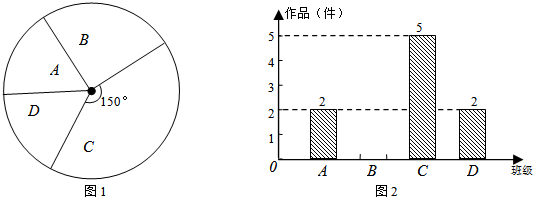
(1)李老师采取的调查方式是
抽样调查
抽样调查
(填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共12
12
件,其中B班征集到作品3
3
,请把图2补充完整.(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要在抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)

分析:(1)根据题意得到此次调查为抽样调查,用C的度数除以360度求出所占的百分比,由C的件数除以所占的百分比即可得到调查的总件数;进而求出B的件数;
(2)画树状图得出所有等可能的情况数,找出一男一女的情况数,即可求出所求的概率.
(2)画树状图得出所有等可能的情况数,找出一男一女的情况数,即可求出所求的概率.
解答:解:(1)此次调查为抽样调查;
根据题意得调查的总件数为:5÷
=12(件),
B的件数为12-(2+5+2)=3(件);补全图2,如图所示:
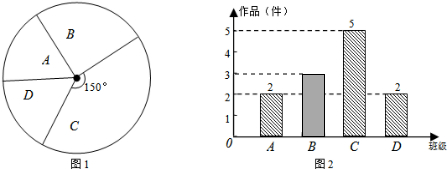
故答案为:抽样调查;12;3;
(2)画树状图如下:
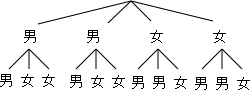
所有等可能的情况有12种,其中一男一女有8种,
则P=
=
.
根据题意得调查的总件数为:5÷
| 150 |
| 360 |
B的件数为12-(2+5+2)=3(件);补全图2,如图所示:

故答案为:抽样调查;12;3;
(2)画树状图如下:

所有等可能的情况有12种,其中一男一女有8种,
则P=
| 8 |
| 12 |
| 2 |
| 3 |
点评:此题考查了条形统计图,扇形统计图,概率的计算,以及用样本估计总体,弄清题意是解本题的关键.

练习册系列答案
相关题目
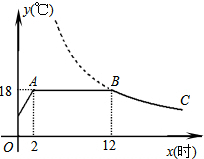 (2013•益阳)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线
(2013•益阳)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线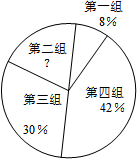 (2013•荆州)我市某中学为备战省运会,在校运动队的学生中进行了全能选手的选拔,并将参加选拔学生的综合成绩分成四组,绘成了如下尚不完整的统计图表.
(2013•荆州)我市某中学为备战省运会,在校运动队的学生中进行了全能选手的选拔,并将参加选拔学生的综合成绩分成四组,绘成了如下尚不完整的统计图表. (2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:
(2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据: