题目内容
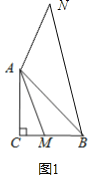
【题目】如图1,△ABC中,∠ACB=90°,AC=BC=![]() ,M为BC边上的一个动点(不与点B,C重合),连接AM,以点A为中心,将线段AM逆时针旋转135°,得到线段AN,连接BN.
,M为BC边上的一个动点(不与点B,C重合),连接AM,以点A为中心,将线段AM逆时针旋转135°,得到线段AN,连接BN.

(1)依题意补全图2;
(2)求证:∠BAN=∠AMB;
(3)点P在线段BC的延长线上,点M关于点P的对称点为Q,写出一个PC的值,使得对于任意的点M,总有AQ=BN,并证明.
【答案】(1)图见解析;(2)证明见解析;(3)![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据旋转图形、线段的画法作图即可;
(2)先证明![]() ,再由三角形内角和求得∠AMB与∠BAM的数量关系,再利用角的和差也可求得∠BAN与∠BAM的关系,进而得结论;
,再由三角形内角和求得∠AMB与∠BAM的数量关系,再利用角的和差也可求得∠BAN与∠BAM的关系,进而得结论;
(3)如图2,任取满足条件的点M,作点M关于点C的对称点![]() ,连接
,连接![]() ,先根据对称性和旋转的性质可知,
,先根据对称性和旋转的性质可知,![]() ,再根据等腰三角形的性质可得
,再根据等腰三角形的性质可得![]() ,从而可得
,从而可得![]() ,又根据线段的和差、对称性得出
,又根据线段的和差、对称性得出![]() ,要总有
,要总有![]() ,只需
,只需![]() 恒成立,然后根据三角形全等的判定定理与性质即可得.
恒成立,然后根据三角形全等的判定定理与性质即可得.
(1)由旋转图形、线段的画法作图如下:
(2)∵![]()
∴![]()
∵![]() ,即
,即![]()
∴![]()
由旋转的定义可知,![]()
∴![]()
∴![]() ;
;
(3)∵![]()
∴![]()
如图2,任取满足条件的点M,作点M关于点C的对称点![]() ,连接
,连接![]()
由对称性和旋转的性质可知,![]()
∴![]()
∴![]()
∵点M关于点P的对称点为Q
∴![]()
∴![]()
要总有![]() ,只需
,只需![]() 恒成立
恒成立
由![]() 定理可知,当
定理可知,当![]() 时,可证出
时,可证出![]()
![]()
解得![]()
因此,当![]() 时,必有
时,必有![]() ,由
,由![]() 定理可证
定理可证![]() ,此时,对于任意的点M,总有
,此时,对于任意的点M,总有![]() .
.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目