题目内容
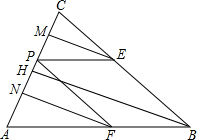 (2013•郴州)如图,△ABC中,AB=BC,AC=8,tanA=k,P为AC边上一动点,设PC=x,作PE∥AB交BC于E,PF∥BC交AB于F.
(2013•郴州)如图,△ABC中,AB=BC,AC=8,tanA=k,P为AC边上一动点,设PC=x,作PE∥AB交BC于E,PF∥BC交AB于F.(1)证明:△PCE是等腰三角形;
(2)EM、FN、BH分别是△PEC、△AFP、△ABC的高,用含x和k的代数式表示EM、FN,并探究EM、FN、BH之间的数量关系;
(3)当k=4时,求四边形PEBF的面积S与x的函数关系式.x为何值时,S有最大值?并求出S的最大值.
分析:(1)根据等边对等角可得∠A=∠C,然后根据两直线平行,同位角相等求出∠CPE=∠A,从而得到∠CPE=∠C,即可得证;
(2)根据等腰三角形三线合一的性质求出CM=
CP,然后求出EM,同理求出FN、BH的长,再根据结果整理可得EM+FN=BH;
(3)分别求出EM、FN、BH,然后根据S△PCE,S△APF,S△ABC,再根据S=S△ABC-S△PCE-S△APF,整理即可得到S与x的关系式,然后利用二次函数的最值问题解答.
(2)根据等腰三角形三线合一的性质求出CM=
| 1 |
| 2 |
(3)分别求出EM、FN、BH,然后根据S△PCE,S△APF,S△ABC,再根据S=S△ABC-S△PCE-S△APF,整理即可得到S与x的关系式,然后利用二次函数的最值问题解答.
解答:(1)证明:∵AB=BC,
∴∠A=∠C,
∵PE∥AB,
∴∠CPE=∠A,
∴∠CPE=∠C,
∴△PCE是等腰三角形;
(2)解:∵△PCE是等腰三角形,EM⊥CP,
∴CM=
CP=
,tanC=tanA=k,
∴EM=CM•tanC=
•k=
,
同理:FN=AN•tanA=
•k=4k-
,
由于BH=AH•tanA=
×8•k=4k,
而EM+FN=
+4k-
=4k,
∴EM+FN=BH;
(3)解:当k=4时,EM=2x,FN=16-2x,BH=16,
所以,S△PCE=
x•2x=x2,S△APF=
(8-x)•(16-2x)=(8-x)2,S△ABC=
×8×16=64,
S=S△ABC-S△PCE-S△APF,
=64-x2-(8-x)2,
=-2x2+16x,
配方得,S=-2(x-4)2+32,
所以,当x=4时,S有最大值32.
∴∠A=∠C,
∵PE∥AB,
∴∠CPE=∠A,
∴∠CPE=∠C,
∴△PCE是等腰三角形;
(2)解:∵△PCE是等腰三角形,EM⊥CP,
∴CM=
| 1 |
| 2 |
| x |
| 2 |
∴EM=CM•tanC=
| x |
| 2 |
| kx |
| 2 |
同理:FN=AN•tanA=
| 8-x |
| 2 |
| kx |
| 2 |
由于BH=AH•tanA=
| 1 |
| 2 |
而EM+FN=
| kx |
| 2 |
| kx |
| 2 |
∴EM+FN=BH;
(3)解:当k=4时,EM=2x,FN=16-2x,BH=16,
所以,S△PCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S=S△ABC-S△PCE-S△APF,
=64-x2-(8-x)2,
=-2x2+16x,
配方得,S=-2(x-4)2+32,
所以,当x=4时,S有最大值32.
点评:本题考查了等腰三角形的判定与性质,平行线的性质,锐角三角函数,二次函数的最值问题,表示出各三角形的高线是解题的关键,也是本题的难点.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 (2013•郴州)如图,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
(2013•郴州)如图,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形. (2013•郴州)如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于( )
(2013•郴州)如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于( )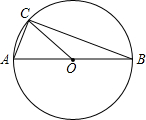 (2013•郴州)如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB=
(2013•郴州)如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB= (2013•郴州)如图,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O为原点,OC、OA所在直线为轴建立坐标系.抛物线顶点为A,且经过点C.点P在线段AO上由A向点O运动,点Q在线段OC上由C向点O运动,QD⊥OC交BC于点D,OD所在直线与抛物线在第一象限交于点E.
(2013•郴州)如图,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O为原点,OC、OA所在直线为轴建立坐标系.抛物线顶点为A,且经过点C.点P在线段AO上由A向点O运动,点Q在线段OC上由C向点O运动,QD⊥OC交BC于点D,OD所在直线与抛物线在第一象限交于点E.