题目内容
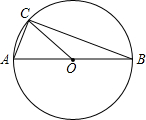（2013•郴州）如图，AB是⊙O的直径，点C是圆上一点，∠BAC=70°，则∠OCB=20
20
°．分析：根据圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半得：∠BOC=2∠BAC，在等腰三角形OBC中可求出∠OCB．
解答：解：∵⊙O是△ABC的外接圆，∠BAC=70°，
∴∠B0C=2∠BAC=2×70°=140°，
∵OC=OB（都是半径），
∴∠OCB=∠OBC=
（180°-∠BOC）=20°．
故答案为：20°．
∴∠B0C=2∠BAC=2×70°=140°，
∵OC=OB（都是半径），
∴∠OCB=∠OBC=
| 1 |
| 2 |
故答案为：20°．
点评：此题考查了圆周角定理，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
（2013•郴州）如图，已知BE∥DF，∠ADF=∠CBE，AF=CE，求证：四边形DEBF是平行四边形．
（2013•郴州）如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（ ）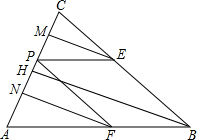
（2013•郴州）如图，△ABC中，AB=BC，AC=8，tanA=k，P为AC边上一动点，设PC=x，作PE∥AB交BC于E，PF∥BC交AB于F．
（2013•郴州）如图，在直角梯形AOCB中，AB∥OC，∠AOC=90°，AB=1，AO=2，OC=3，以O为原点，OC、OA所在直线为轴建立坐标系．抛物线顶点为A，且经过点C．点P在线段AO上由A向点O运动，点Q在线段OC上由C向点O运动，QD⊥OC交BC于点D，OD所在直线与抛物线在第一象限交于点E．