Question

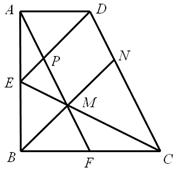
如图，已知直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2AD，点E、F分别是AB、BC边的中点，连接AF、CE交于点M，连接BM并延长交CD于点N，连接DE交AF于点P，则结论：①∠ABN=∠CBN； ②DE∥BN； ③△CDE是等腰三角形； ④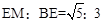； ⑤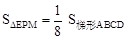，正确的个数有【    】

 A.  5个      B. 4个       C.  3个      D. 2个

 

Answer 1

【答案】

B。

【解析】如图，连接DF，AC，EF，

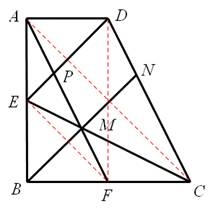
∵E、F分别为AB、BC的中点，且AB=BC，

∴AE=EB=BF=FC。

在△ABF和△CBE中，∵AB=CB，∠ABF=∠CBE， BF=BE，

∴△ABF≌△CBE（SAS）。∴∠BAF=∠BCE，AF=CE。

在△AME和△CMF中，

∵∠BAF=∠BCE，∠AME=∠CMF ，AE=CF，

∴△AME≌△CMF（AAS）。∴EM=FM。

在△BEM和△BFM中，∵BE=BF，BM=BM， EM=FM，∴△BEM≌△BFM（SSS）。

∴∠ABN=∠CBN。结论①正确。

∵AE=AD，∠EAD=90°，∴△AED为等腰直角三角形。∴∠AED=45°。

∵∠ABC=90°，∴∠ABN=∠CBN=45°。∴∠AED=∠ABN=45°。

∴ED∥BN。结论②正确。

∵AB=BC=2AD，且BC=2FC，∴AD=FC。

又∵AD∥FC，∴四边形AFCD为平行四边形。∴AF=DC。

又AF=CE，∴DC=EC。则△CED为等腰三角形。结论③正确。

∵EF为△ABC的中位线，∴EF∥AC，且EF=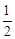AC。

∴∠MEF=∠MCA，∠EFM=∠MAC。∴△EFM∽△CAM。∴EM：MC=EF：AC=1：2。

设EM=x，则有MC=2x，EC=EM+MC=3x，

设EB=y，则有BC=2y，

在Rt△EBC中，根据勾股定理得：，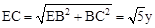

∴3x=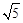y，即x：y=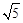：3。∴EM：BE=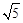：3。结论④正确。

∵E为AB的中点，EP∥BM，∴P为AM的中点。

∴。

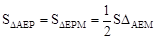又∵，∴。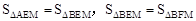

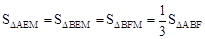∵四边形ABFD为矩形，∴。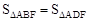

又∵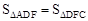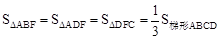，∴S。

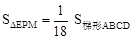∴。结论⑤错误。

因此正确的个数有4个。故选B。