题目内容
如图,二次函数 的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
(1)求二次函数的解析式;
(2)设点D的坐标为(x,y),试求矩形ABCD的周长P关于自变量x的函数解析式,并求出自变量x的取值范围;
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论。
(1) y=-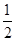 x2+2;(2)p=-(x+2)2+8,其中-2<x<2;(3)不存在,证明见解析.
x2+2;(2)p=-(x+2)2+8,其中-2<x<2;(3)不存在,证明见解析.
解析试题分析:(1)由顶点坐标(0,2)可直接代入y=-mx2+4m,求得m=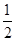 ,即可求得抛物线的解析式;
,即可求得抛物线的解析式;
(2)由图及四边形ABCD为矩形可知AD∥x轴,长为2x的据对值,AB的长为A点的总坐标,由x与y的关系,可求得p关于自变量x的解析式,因为矩形ABCD在抛物线里面,所以x小于0,大于抛物线与x负半轴的交点;
(3)由(2)得到的p关于x的解析式,可令p=9,求x的方程,看x是否有解,有解则存在,无解则不存在,显然不存在这样的p.
试题解析:(1)∵二次函数y=-mx2+4m的顶点坐标为(0,2),
∴4m=2,
即m=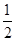 ,
,
∴抛物线的解析式为:y=-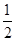 x2+2;
x2+2;
(2)∵D点在x轴的正方向上坐标为(x,y),四边形ABCD为矩形,BC在x轴上,
∴AD∥x轴,
又由抛物线关于y轴对称,
所以D、C点关于y轴分别与A、B对称.
所以AD的长为2x,AB长为y,
所以周长p=2y+4x=2(-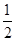 x2+2)-4x=-(x+2)2+8.
x2+2)-4x=-(x+2)2+8.
∵D在抛物线上,且ABCD组成矩形,
∴x<2,
∵四边形ABCD为矩形,
∴y>0,
即x>-2.
所以p=-(x+2)2+8,其中-2<x<2.
(3)不存在,
证明:假设存在这样的p,即:9=-(x+2)2+8,
解此方程得:x无解,所以不存在这样的p.
考点: 二次函数综合题.

 全能闯关100分系列答案
全能闯关100分系列答案某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:
| | 每件T恤的利润(元) | 销售量(件) |
| 第一个月 | | |
| 清仓时 | | |
 元,出厂价为每件
元,出厂价为每件 元,每月销售量
元,每月销售量 (件)与销售单价
(件)与销售单价 (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数:  .
. 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元? (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润? 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元?
 的代数式表示);
的代数式表示); 与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
 x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.