题目内容
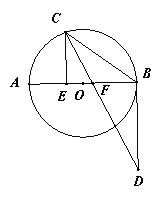
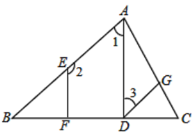
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若AE=4,AD=5,求OE的长.

【答案】(1)见解析;(2)OE=![]() .
.
【解析】
(1)根据菱形的性质得到AD∥BC,推出四边形AECF是平行四边形,根据矩形的判定定理即可得到结论;
(2)根据勾股定理得到BE=3,AC=![]() ,然后根据直角三角形斜边的中线性质可得到结论.
,然后根据直角三角形斜边的中线性质可得到结论.
(1)证明:∵菱形ABCD,
∴AD∥BC.
∵CF∥AE,
∴四边形AECF是平行四边形.
∵AE⊥BC,
∴平行四边形AECF是矩形.
(2)解:∵AE=4,AD=5,
∴AB=5,BE=3.
∵AB=BC=5,
∴CE=8.
∴AC=![]() .
.
∵对角线AC,BD交于点O,
∴AO=CO=![]() .
.
∴OE=![]() .
.


练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
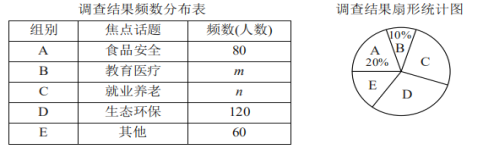
【题目】实验中学捐资购买了一批物资240吨打算扶贫山区。现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示(每辆车均装满)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨) | 10 | 16 | 20 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元。求甲、乙两种车型各多少辆?
(2)为了节约运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知三种车辆总数为14辆。请求出三种车型分别是多少辆?此时的运费又是多少元?