题目内容
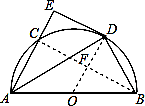
【题目】如图所示,AB为半圆O的直径,C为圆上一点,AD平分∠BAC交半圆于点D,过点D作DE⊥AC,DE交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,DE= ![]() ,求线段AC的长
,求线段AC的长
【答案】
(1)证明:连接OD,
∵OA=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAD,
∴AE∥OD,
∴∠AED+∠EDO=180°,
∵DE⊥AC,
∴∠EDO=90°,
∴DE是⊙O的切线;
(2)解:连接BC交OD于F,
∵AB为直径,
∴∠ACB=90°,
∵∠AED=∠EDO=90°,
∴四边形DECF为矩形,
∴DE=CF= ![]() ,∠DFC=90°,
,∠DFC=90°,
∴OD⊥BC,
∴BC=2CF=2 ![]() ,
,
∵AB=4,
∴AC= ![]() =2.
=2.
【解析】(1)证切线需要证明该线垂直于过切点的半径,所以我们首先要连接OD,并进一步利用平行线性质,互补关系,证明∠EDO=90°
(2)利用垂径定理结合矩形性质可得DE=CF= ![]() ,BC=2CF=2
,BC=2CF=2 ![]() ,再利用勾股定理易得AC=
,再利用勾股定理易得AC= ![]() =2.
=2.

练习册系列答案
相关题目