题目内容
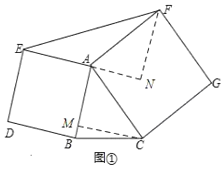
【题目】(1)如图①,分别以△ABC的边AB、AC为一边向形外作正方形ABDE和正方形ACGF.求证S△AEF=S△ABC.
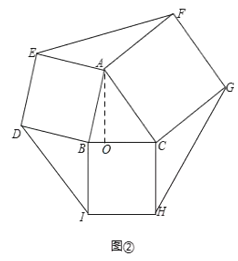
(2)如图②,分别以△ABC的边AB、AC、BC为边向形外作正方形ABDE、ACGF、BCHI,可得六边形DEFGHI,若S正方形ABDE=17,S正方形ACGF=25,S正方形BCHI=16,求S六边形DEFGHI.

【答案】(1)证明见解析;(2)90.
【解析】
(1)过点C作CM⊥AB,过F作FN⊥EA与EA的延长线交于点N,求出∠CAM=∠FAN,然后证明△AMC≌△ANF(AAS),得到CM=FN,根据三角形面积公式可得结论;
(2)由(1)可得:S△AEF=S△ABC=S△BDI=S△CHG,过点A作AO⊥BC于O,设BO=x,则CO=4x,根据勾股定理列方程得:17x2=25(4x)2,解得x=1,求出AO,根据面积和可得S六边形DEFGHI.
证明:(1)如图①,过点C作CM⊥AB,过F作FN⊥EA与EA的延长线交于点N,
∴∠CMA=∠ANF=90°,
∵四边形ABDE和四边形ACGF是正方形,
∴AB=AE,AC=AF,∠BAE=∠BAN=∠CAF=90°,
∴∠CAM+∠CAN=∠FAN+∠CAN=90°,
∴∠CAM=∠FAN,
在△AMC和△ANF中,
∵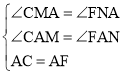 ,
,
∴△AMC≌△ANF(AAS),
∴CM=FN,
∴![]() AEFN=
AEFN=![]() ,
,
∴S△AEF=S△ABC;
(2)由上题结论得:S△AEF=S△ABC=S△BDI=S△CHG,
∵S正方形ABDE=17,S正方形ACGF=25,S正方形BCHI=16,
∴AB=![]() ,AC=5,BC=4,
,AC=5,BC=4,
过点A作AO⊥BC于O,设BO=x,则CO=4﹣x,
在Rt△ABO和Rt△ACO中,AO2=AB2﹣BO2=AC2﹣CO2,即17﹣x2=25﹣(4﹣x)2,
解得:x=1,即BO=1,
∴![]() ,
,
S六边形DEFGHI=S正方形ABDE+S正方形BCHI+S正方形ACGF+S△AEF+S△BDI+S△CHG+S△ABC,
=17+25+16+4×![]() ×4×4,
×4×4,
=90.