题目内容
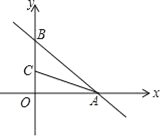
【题目】在平面直角坐标系中，已知一次函数y=﹣
x+6与x，y轴分别交于A，B两点，点C（0，n）是y轴上一点，把坐标平面沿直线AC折叠，点B刚好落在x轴上，则点C的坐标是（ ）
A. （0，3） B. （0，
） C. （0，
） D. （0，
）
【答案】C
【解析】
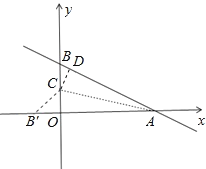
过C作CD⊥AB于D，先求出A，B的坐标，分别为A（8，0），B（0，6），得到AB的长，再根据折叠的性质得到AC平分∠OAB，得到CD=CO=n，DA=OA=8，则DB=10-8=2，BC=6-n，在Rt△BCD中，利用勾股定理得到n的方程，解方程求出n即可．
过C作CD⊥AB于D，如图，
对于直线y=
x+6，
当x=0，得y=6；当y=0，x=8，
∴A(8,0),B(0,6)，即OA=8，OB=6，
∴AB=10，
又∵坐标平面沿直线AC折叠，使点B刚好落在x轴上，
∴AC平分∠OAB，
∴CD=CO=n，则BC=6n，
∴DA=OA=8，
∴DB=108=2，
在Rt△BCD中,DC2+BD2=BC2，
∴n2+22=(6n)2,解得n=
，
∴点C的坐标为(0,).
故选：C.
阳光试卷单元测试卷系列答案
【题目】如图，P是正△ABC内的一点，且PA=6，PB=8，PC=10．若将△PAC绕点A逆时针旋转后，得到△P′AB． 
（1）求旋转角的度数；
（2）求点P与点P′之间的距离；
（3）求∠APB的度数．
【题目】某蒜薹生产基地喜获丰收，收获蒜薹200吨．经市场调查，可采用批发、零售、冷库储藏后销售三种方式，并按这三种方式销售，计划平均每吨的售价及成本如下表：
销售方式 | 批发 | 零售 | 储藏后销售 |
售价（元/吨） | 3000 | 4500 | 5500 |
成本（元/吨） | 700 | 1000 | 1200 |
若经过一段时间，蒜薹按计划全部售出获得的总利润为y（元），蒜薹零售x（吨），且零售量是批发量的
．
（1）求y与x之间的函数关系式；
（2）由于受条件限制，经冷库储藏售出的蒜薹最多80吨，求该生产基地按计划全部售完蒜薹获得的最大利润．
