题目内容
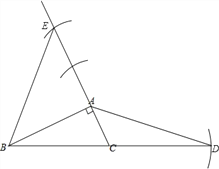
【题目】已知:如图,Rt△ABC中,∠BAC=90°.
(1)按要求作图:(保留作图痕迹)

①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
解:(1)AD与BE的大小关系是________________.
(2)证明:
【答案】(1)AD=BE ;(2)详见解析.
【解析】试题分析:(1)根据基本作图,作一条线段等于已知线段的作图方法就可以作出图形;
(2)延长AC到点F,使CF=AF,连接BF,证明△ACD≌△FCB,就有AD=FB,进而得出AE=AF,就可以得出BE=BF,从而结论AD=BE.
试题解析:(1)由题意,得作图如下:
(2)延长AC到点F,使CF=AF,连接BF,
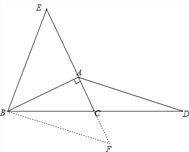
在△ACD和△FCB中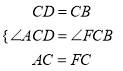 ,
,
∴△ACD≌△FCB(SAS)
∴AD=FB.
∵CF=AC,
∴AF=2AC.
∵AE=2CA,
∴AF=AE,
∵∠BAC=90°,
∴AB⊥EF,
∴AB是EF的垂直平分线,
∴BE=BF,
∴AD=BE.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目




